题目内容
（2011•东城区一模）已知平面上不重合的四点P，A，B，C满足
+
+
=0，且
+
=m
，那么实数m的值为（ ）
| PA |
| PB |
| PC |
| AB |
| AC |
| AP |
分析：利用向量基本定理结合向量的减法有：
=
-
，
=
-
，代入化简即得．
| AB |
| PB |
| PA |
| AC |
| PC |
| PA |
解答：解：由题意得，向量的减法有：
=
-
，
=
-
，
∴(
-
)+(
-
)=-m
；
∴(m-2)
+
+
=
，
对照条件
+
+
=0，
∴m-2=1，
∴m=3．
故选B．
| AB |
| PB |
| PA |
| AC |
| PC |
| PA |
∴(
| PB |
| PA |
| PC |
| PA |
| PA |
∴(m-2)
| PA |
| PB |
| PC |
| 0 |
对照条件
| PA |
| PB |
| PC |
∴m-2=1，
∴m=3．
故选B．
点评：本小题主要考查平面向量的基本定理及其意义、向量数乘的运算及其几何意义等基础知识．本题的计算中，只需将向量都化成以P为起点就可以比较得出解答了，解答的关键是向量基本定理的理解与应用．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
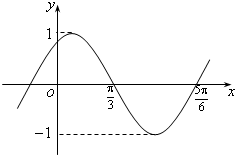（2011•东城区一模）已知函数y=sin（ωx+φ）
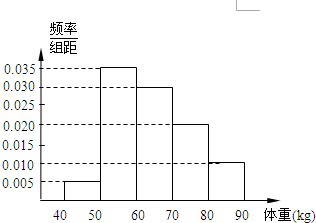（2011•东城区一模）从某地高中男生中随机抽取100名同学，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．由图中数据可知体重的平均值为