题目内容
已知椭圆
的两个焦点为F1，F2，椭圆上一点M
满足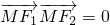
．
（1）求椭圆的方程；
（2）若直线L：y=
与椭圆恒有不同交点A、B，且
（O为坐标原点），求k的范围．
解：（1）由题意得：
c=
，a=2，
∴b=1．
∴椭圆方程为
（2）由
，
设A（x1，y1），B（x2，y2）
则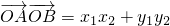
=
，
∴
．
分析：（1）由题意得：c=，a=2，b=1．从而写出椭圆方程即可；
（2）将直线的方程代入椭圆的方程，消去y得到关于x的一元二次方程，再结合根系数的关系利用向量的数量积坐标公式即可求得k的范围，从而解决问题．
点评：本小题主要考查椭圆的应用、向量的数量积的应用、不等式的解法等基础知识，解答的关键在于学生的运算求解能力，数形结合思想、化归与转化思想．属于基础题．
c=
，a=2，∴b=1．
∴椭圆方程为
（2）由
，设A（x1，y1），B（x2，y2）
则
=
，∴
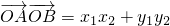
．分析：（1）由题意得：c=
，a=2，b=1．从而写出椭圆方程即可；（2）将直线的方程代入椭圆的方程，消去y得到关于x的一元二次方程，再结合根系数的关系利用向量的数量积坐标公式即可求得k的范围，从而解决问题．
点评：本小题主要考查椭圆的应用、向量的数量积的应用、不等式的解法等基础知识，解答的关键在于学生的运算求解能力，数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
），（1，0），椭圆的长半轴长为2，则椭圆方程为（ ）
B．
D．
的两个焦点为F1、F2，椭圆上一点
满足
与椭圆恒有两上不同的交点A、B，且
（O是坐标原点），求k的范围。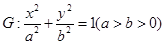
的两个焦点为
、
，点
在椭圆G上，且
，且
，斜率为1的直线
与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为P（-3,2）.
的面积.
，
，
是椭圆上一点，
，
，则该椭圆的方程是( ) 
B、
C、
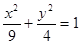D、