题目内容
已知椭圆与双曲线2x2-2y2=1共焦点,且过(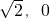 )
)
(1)求椭圆的标准方程.
(2)求斜率为2的一组平行弦的中点轨迹方程.
解:(1)依题意得,将双曲线方程标准化为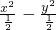 =1,则c=1.
=1,则c=1.
∵椭圆与双曲线共焦点,∴设椭圆方程为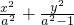 =1,∵椭圆过(
=1,∵椭圆过( ,0),
,0),
∴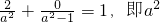 =2,∴椭圆方程为
=2,∴椭圆方程为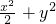 =1.
=1.
(2)依题意,设斜率为2的弦所在直线的方程为y=2x+b,弦的中点坐标为(x,y),则
y=2x+b 且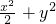 =1得,9x2+8xb+2b2-2=0,∴x1+x2=-
=1得,9x2+8xb+2b2-2=0,∴x1+x2=-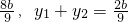 .
.
即x=-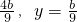 两式消掉b得 y=-
两式消掉b得 y=- x.
x.
令△=0,64b2-36(2b2-2)=0,即b=±3,所以斜率为2且与椭圆相切的直线方程为y=2x±3
即当x=± 时斜率为2的直线与椭圆相切.
时斜率为2的直线与椭圆相切.
所以平行弦得中点轨迹方程为:y=- x(-
x(-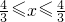 ).
).
分析:(1)求出双曲线的焦点,由此设出椭圆方程,把点( ,0)代入椭圆方程,求出待定系数即得所求的椭圆方程.
,0)代入椭圆方程,求出待定系数即得所求的椭圆方程.
(2)设斜率为2的弦所在直线的方程为y=2x+b,弦的中点坐标为(x,y),把y=2x+b 代入椭圆的方程,利用一元二次方程根与系数的关系,求出轨迹方程为y=- x,求出直线y=2x+b 和椭圆相切时的b值,即得轨迹方程中自变量x
x,求出直线y=2x+b 和椭圆相切时的b值,即得轨迹方程中自变量x
的范围.
点评:本题考查用待定系数法求椭圆的标准方程,以及简单性质的应用;求点的轨迹方程的方法,求轨迹方程中自变量x的范围,是解题的易错点.
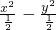 =1,则c=1.
=1,则c=1.∵椭圆与双曲线共焦点,∴设椭圆方程为
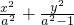 =1,∵椭圆过(
=1,∵椭圆过( ,0),
,0),∴
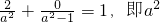 =2,∴椭圆方程为
=2,∴椭圆方程为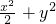 =1.
=1.(2)依题意,设斜率为2的弦所在直线的方程为y=2x+b,弦的中点坐标为(x,y),则
y=2x+b 且
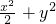 =1得,9x2+8xb+2b2-2=0,∴x1+x2=-
=1得,9x2+8xb+2b2-2=0,∴x1+x2=-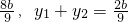 .
.即x=-
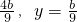 两式消掉b得 y=-
两式消掉b得 y=- x.
x.令△=0,64b2-36(2b2-2)=0,即b=±3,所以斜率为2且与椭圆相切的直线方程为y=2x±3
即当x=±
 时斜率为2的直线与椭圆相切.
时斜率为2的直线与椭圆相切.所以平行弦得中点轨迹方程为:y=-
 x(-
x(-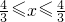 ).
).分析:(1)求出双曲线的焦点,由此设出椭圆方程,把点(
 ,0)代入椭圆方程,求出待定系数即得所求的椭圆方程.
,0)代入椭圆方程,求出待定系数即得所求的椭圆方程.(2)设斜率为2的弦所在直线的方程为y=2x+b,弦的中点坐标为(x,y),把y=2x+b 代入椭圆的方程,利用一元二次方程根与系数的关系,求出轨迹方程为y=-
 x,求出直线y=2x+b 和椭圆相切时的b值,即得轨迹方程中自变量x
x,求出直线y=2x+b 和椭圆相切时的b值,即得轨迹方程中自变量x的范围.
点评:本题考查用待定系数法求椭圆的标准方程,以及简单性质的应用;求点的轨迹方程的方法,求轨迹方程中自变量x的范围,是解题的易错点.

练习册系列答案
相关题目
 的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形;
的两个焦点为F1,F2,则这个椭圆上存在六个不同的点M,使得△F1MF2为直角三角形; 的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a;
的一个焦点作它的一条渐近线的垂线,垂足为M,O为坐标原点,则|OM|=a; 相交于A、B两点.
相交于A、B两点. 上的任意两点,M是线段AB的中点,若直线AB、OM的斜率都存在,并记为kAB,kOM,则kAB?kOM为定值.试对双曲线
上的任意两点,M是线段AB的中点,若直线AB、OM的斜率都存在,并记为kAB,kOM,则kAB?kOM为定值.试对双曲线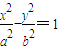 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.