题目内容
若函数 为奇函数(a为常数).
为奇函数(a为常数).(1)求a的值;
(2)用函数单调性定义证明函数f(x)在区间(1,+∞)上单调递增.
【答案】分析:(1)由于已知函数是奇函数,根据奇函数的定义可得f(-x)+f(x)=0,结合对数的运算性质解方程可得a的值;
(2)由(1)得函数的解析式,设x1,x2∈(1,+∞)且x1<x2,根据对数的性质,判断f(x1)-f(x2)与0的关系,进而根据单调性的定义,可得答案.
解答:解:(1)∵函数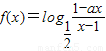 为奇函数
为奇函数
∴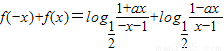 =
=
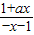 •
•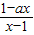 =0
=0
即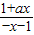 •
•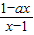 =1
=1
解得a=-1 (6分)
(2)设x1,x2∈(1,+∞)且x1<x2,
∴2x2-2x1>0
∴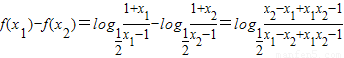
又∵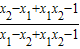 >1
>1
∴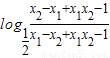 <0
<0
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴函数f(x)在区间(1,+∞)内单调递增. (14分)
点评:本题考查的知识点是对数函数的图象和性质,函数的奇偶性和函数的单调性,其中熟练掌握函数奇偶性与单调性的定义是解答本题的关键.
(2)由(1)得函数的解析式,设x1,x2∈(1,+∞)且x1<x2,根据对数的性质,判断f(x1)-f(x2)与0的关系,进而根据单调性的定义,可得答案.
解答:解:(1)∵函数
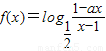 为奇函数
为奇函数∴
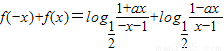 =
=
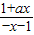 •
•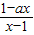 =0
=0即
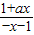 •
•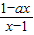 =1
=1解得a=-1 (6分)
(2)设x1,x2∈(1,+∞)且x1<x2,
∴2x2-2x1>0
∴
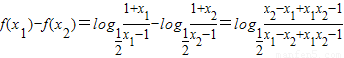
又∵
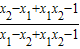 >1
>1∴
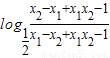 <0
<0∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴函数f(x)在区间(1,+∞)内单调递增. (14分)
点评:本题考查的知识点是对数函数的图象和性质,函数的奇偶性和函数的单调性,其中熟练掌握函数奇偶性与单调性的定义是解答本题的关键.

练习册系列答案
相关题目
 为奇函数(a为常数).
为奇函数(a为常数). 为奇函数(a为常数).
为奇函数(a为常数).