题目内容
4.三棱锥P-ABC中,∠APB=∠BPC=∠CPA=90°,M在△ABC内,∠MPA=∠MPB=60°,则∠MPC=45°.分析 过M做平面PBC的垂线,交平面PBC于Q,连接PQ,由公式:cos∠MPB=cos∠MPQ×cos∠QPB,得到cos∠QPB=$\frac{\sqrt{6}}{3}$,从而可得cos∠QPC=$\frac{\sqrt{3}}{3}$,再用公式:cos∠MPC=cos∠MPQ×cos∠QPC,即可求∠MPC.
解答 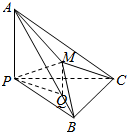 解:如图,过M做平面PBC的垂线,交平面PBC于Q,连接PQ.
解:如图,过M做平面PBC的垂线,交平面PBC于Q,连接PQ.
∵∠APB=∠APC=90°,∴AP⊥平面PBC,
∵MQ⊥平面PBC,∴AP∥MQ,
∵∠MPA=60°,∴∠MPQ=90°-60°=30°.
由公式:cos∠MPB=cos∠MPQ×cos∠QPB,得到cos∠QPB=$\frac{\sqrt{6}}{3}$.
∵∠QPC是∠QPB的余角,∴cos∠QPC=$\frac{\sqrt{3}}{3}$.
再用公式:cos∠MPC=cos∠MPQ×cos∠QPC,得到cos∠MPC=$\frac{\sqrt{2}}{2}$.
∴∠MPC=45°.
故答案为:45°.
点评 本题考查空间角,考查学生分析解决问题的能力,利用好公式是关键,是中档题.

练习册系列答案
相关题目
19.已知三棱柱ABC-A1B1C1的底面是正三角形,所有棱长都是6,顶点A1在底面ABC内的射影是△ABC的中心,则四面体A1ABC,B1ABC,C1ABC公共部分的体积等于( )
| A. | 6$\sqrt{2}$ | B. | 6$\sqrt{3}$ | C. | 12$\sqrt{2}$ | D. | 12$\sqrt{3}$ |
9.已知i是虚数单位,设复数z1=1+i,z2=1+2i,则$\frac{{z}_{1}}{{z}_{2}}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.已知A,B为双曲线E的左,右顶点,点M在E上,△ABM为等腰三角形,且顶角为135°,则E的离心率为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\root{4}{2}$ |
13.已知映射f:P→Q是从P到Q的一个函数,则P,Q的元素( )
| A. | 可以是点 | B. | 可以是方程 | C. | 必须是实数 | D. | 可以是三角形 |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°. 如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径$r=\root{3}{10}$毫米,滴管内液体忽略不计.如果瓶内的药液恰好156分钟滴完,则每分钟应滴下75滴.
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径$r=\root{3}{10}$毫米,滴管内液体忽略不计.如果瓶内的药液恰好156分钟滴完,则每分钟应滴下75滴.