题目内容
设向量 ,
, ,
, ,
, ,其中θ∈(0,
,其中θ∈(0, ).
).
(1)求 的取值范围;
的取值范围;
(2)若函数f(x)=|x-1|,比较f( )与f(
)与f(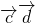 )的大小.
)的大小.
解:(1)∵ =2+cos2θ,
=2+cos2θ,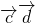 =2sin2θ+1=2-cos2θ,
=2sin2θ+1=2-cos2θ,
∴ =2cos2θ,
=2cos2θ,
∵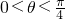 ,∴
,∴ ,∴0<2cos2θ<2,
,∴0<2cos2θ<2,
∴ 的取值范围是(0,2).
的取值范围是(0,2).
(2)∵f( )=|2+cos2θ-1|=|1+cos2θ|=2cos2θ,
)=|2+cos2θ-1|=|1+cos2θ|=2cos2θ,
f(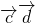 )=|2-|cos2θ-1=|1-cos2θ|=2cos2θ,
)=|2-|cos2θ-1=|1-cos2θ|=2cos2θ,
∴f( )-f(
)-f(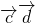 )=2(2cos2θ-2cos2θ)=2cos2θ,
)=2(2cos2θ-2cos2θ)=2cos2θ,
∵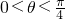 ,∴
,∴ ,∴2cos2θ>0,
,∴2cos2θ>0,
∴f( )>f(
)>f(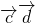 )
)
分析:(1)利用向量数量积的坐标运算将 表达为θ的三角函数,利用二倍角公式去平方,结合余弦函数的图象求范围即可.
表达为θ的三角函数,利用二倍角公式去平方,结合余弦函数的图象求范围即可.
(2)首先将f( )与f(
)与f(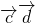 )均表达为θ的函数,分别判断范围,再比较大小即可.
)均表达为θ的函数,分别判断范围,再比较大小即可.
点评:本题考查向量的运算、三角变换及三角函数的性质等知识,熟练的利用三角函数公式进行化简变形时解决此类问题的关键.
 =2+cos2θ,
=2+cos2θ,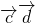 =2sin2θ+1=2-cos2θ,
=2sin2θ+1=2-cos2θ,∴
 =2cos2θ,
=2cos2θ,∵
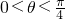 ,∴
,∴ ,∴0<2cos2θ<2,
,∴0<2cos2θ<2,∴
 的取值范围是(0,2).
的取值范围是(0,2).(2)∵f(
 )=|2+cos2θ-1|=|1+cos2θ|=2cos2θ,
)=|2+cos2θ-1|=|1+cos2θ|=2cos2θ,f(
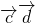 )=|2-|cos2θ-1=|1-cos2θ|=2cos2θ,
)=|2-|cos2θ-1=|1-cos2θ|=2cos2θ,∴f(
 )-f(
)-f(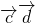 )=2(2cos2θ-2cos2θ)=2cos2θ,
)=2(2cos2θ-2cos2θ)=2cos2θ,∵
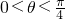 ,∴
,∴ ,∴2cos2θ>0,
,∴2cos2θ>0,∴f(
 )>f(
)>f(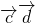 )
)分析:(1)利用向量数量积的坐标运算将
 表达为θ的三角函数,利用二倍角公式去平方,结合余弦函数的图象求范围即可.
表达为θ的三角函数,利用二倍角公式去平方,结合余弦函数的图象求范围即可.(2)首先将f(
 )与f(
)与f(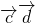 )均表达为θ的函数,分别判断范围,再比较大小即可.
)均表达为θ的函数,分别判断范围,再比较大小即可.点评:本题考查向量的运算、三角变换及三角函数的性质等知识,熟练的利用三角函数公式进行化简变形时解决此类问题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 =
= ,
, =
= ,其中
,其中 =λ
=λ
 =
= ,
, =
= ,其中
,其中 =λ
=λ

 ,
, ,
, ,
, ,其中θ∈(0,
,其中θ∈(0, ).
). 的取值范围;
的取值范围; ,
, ,
, ,
, ,其中θ∈(0,
,其中θ∈(0, ).
). 的取值范围;
的取值范围; ,
, ,
, ,
, ,其中θ∈(0,
,其中θ∈(0, ).
). 的取值范围;
的取值范围;