题目内容
如果以数列
的任意连续三项作边长，都能构成一个三角形，那么称这样的数列为“三角形”数列；又对于“三角形”数列，如果函数y=f(x)使得由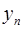
=f(
)(
)确定的数列
仍成为一个“三角形”数列，就称y="f(x)" 是数列的“保三角形”函数。
（Ⅰ）、已知数列
是首项为2012，公比为
的等比数列，求证：是“三角形”数列；
（Ⅱ）、已知数列
是首项为2，公差为1的等差数列，若函数f(x)=
(m＞0且m≠1)是的“保三角形”函数. 求m的取值范围.
的任意连续三项作边长，都能构成一个三角形，那么称这样的数列为“三角形”数列；又对于“三角形”数列，如果函数y=f(x)使得由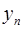=f()()确定的数列仍成为一个“三角形”数列，就称y="f(x)" 是数列的“保三角形”函数。（Ⅰ）、已知数列
是首项为2012，公比为的等比数列，求证：是“三角形”数列；（Ⅱ）、已知数列
是首项为2，公差为1的等差数列，若函数f(x)= (m＞0且m≠1)是的“保三角形”函数. 求m的取值范围.解：（Ⅰ）、是递减数列···2分，
故对任意的正整数n ，
构成三角形当且仅当满足
这显然成立，故是“三角形”数列···6分
（Ⅱ）、
=7n+1··7分
是“三角形”数列
①若0<m<1,则是递减数列，
构成三角形当且仅当满足
···6分
②若m>1, 则是递增数列，可求得
···12分。
故m的取值范围是：或···14分
是递减数列···2分，故对任意的正整数n ，
构成三角形当且仅当满足这显然成立，故
是“三角形”数列···6分（Ⅱ）、
=7n+1··7分是“三角形”数列①若0<m<1,则
是递减数列，构成三角形当且仅当满足 ···6分②若m>1, 则
是递增数列，可求得···12分。故m的取值范围是：
或···14分略
练习册系列答案
相关题目
中，已知
且
，则
_______
}的前
项和
=
（
=1，通过计算
，猜想
；
，则G必是
a与b的等比中项；
是常数数列 a,a,a，·····，则
（a,b,c为实常数），则必有：c=0.
，
，
，
，
，
，
，
，
，
，
，
，…,则第
个数对是（ ）
中，
为数列
项和，且
，则
．
),则an= ( )
中，
，
，则
=