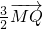题目内容
已知点H(0,-3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程;
(2)过定点A(a,b)的直线与曲线C相交于两点S R,求证:抛物线S R两点处的切线的交点B恒在一条直线上.
分析:(1)设出P,Q的坐标,利用
•
=0求得a和b的关系,设出M的坐标,利用
=-
,可求得x和y的表达式,消去b,进而求得x和y的关系式.
(2)设出A,S,R,则可表示SR的方程把点A代入SR,同时对曲线C的方程求导,判断出SR处的切线方程,最后联立方程求得ax-2y-2b=0判断出B点在直线.
| HP |
| PM |
| PM |
| 3 |
| 2 |
| MQ |
(2)设出A,S,R,则可表示SR的方程把点A代入SR,同时对曲线C的方程求导,判断出SR处的切线方程,最后联立方程求得ax-2y-2b=0判断出B点在直线.
解答:解:(1)设P(a,0),Q(0,b)则:
•
=(a,3)(a,-b)=a2-3b=0
∴a2=3b
设M(x,y)∵
=-
∴x=
=-2a,y=
=3b∴y=
x2
(2)设A(a,b),S(x1,
x12),R(x2,
x22),(x1≠x2)
则直线SR的方程为:y-
x12=
(x-x1),即4y=(x1+x2)x-x1x2
∵A点在SR上,
∴4b=(x1+x2)a-x1x2①
对y=
x2求导得:y′=
x
∴抛物线上SR处的切线方程为
y-
x12=
x1(x-x1)即4y=2x1x-x12②
y-
x22=
x2(x-x2)即4y=2x2x-x22③
联立②③得
代入①得:ax-2y-2b=0故:B点在直线ax-2y-2b=0上
| HP |
| PQ |
∴a2=3b
设M(x,y)∵
| PM |
| 3 |
| 2 |
| HQ |
∴x=
| a | ||
1-
|
-
| ||
1-
|
| 1 |
| 4 |
(2)设A(a,b),S(x1,
| 1 |
| 4 |
| 1 |
| 4 |
则直线SR的方程为:y-
| 1 |
| 4 |
| ||||
| x2-x1 |
∵A点在SR上,
∴4b=(x1+x2)a-x1x2①
对y=
| 1 |
| 4 |
| 1 |
| 2 |
∴抛物线上SR处的切线方程为
y-
| 1 |
| 4 |
| 1 |
| 2 |
y-
| 1 |
| 4 |
| 1 |
| 2 |
联立②③得
|
代入①得:ax-2y-2b=0故:B点在直线ax-2y-2b=0上
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生对问题的综合分析和基本的运算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
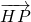 •
• =0,
=0,