题目内容
已知等比数列 满足:
满足: 公比
公比 ,数列
,数列 的前
的前 项和为
项和为 ,且
,且 (
( ).
).
(1)求数列 和数列
和数列 的通项
的通项 和
和 ;
;
(2)设 ,证明:
,证明: .
.
(1) 解法一:由 得,
得,

由上式结合 得
得 ,
,
则当 时,
时,
 ,
,
 -
-
 ,
,
∵ ,∴
,∴ ,
,
∴数列 是首项为
是首项为 ,公比为4的等比数列,
,公比为4的等比数列,
∴ ,∴
,∴ .
.
【解法二:由 得,
得,

由上式结合 得
得 ,
,
则当 时,
时,
 ,
,

 -
-

 ,
,
∴
 ,
,
∵ ,∴
,∴ ,
,
∴ .-
.-
(2) 由 得
得 ,-
,-


 -
-
【或 】
】
∴

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 中的
中的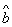 的值为
的值为 ,则记忆力为14的同学的判断力约为(附:线性回归方程
,则记忆力为14的同学的判断力约为(附:线性回归方程 中,
中, ,
,
其中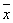 ,
, 为样本平均值)
为样本平均值)
A.7 B. C.8 D.
C.8 D.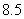
 x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)
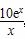 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403) ,则s
,则s 的最大值为 。
的最大值为 。 为偶函数,且
为偶函数,且 若函数
若函数 ,则
,则 = .
= . ,
, ,
, ,则
,则  B.
B.  C.
C. D.
D.
 到极轴的距离是
到极轴的距离是
 ,满足条件
,满足条件 的函数是
的函数是 (B)
(B) (C)
(C) (D)
(D)
 的值是( )
的值是( ) B.
B. C.
C. D.
D.