题目内容
设直线 :
: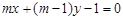 ,圆
,圆 :
: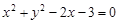 ,则( )
,则( )
A.对任意实数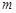 ,直线 ,直线 恒过定点 恒过定点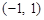 |
B.存在实数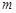 ,使直线 ,使直线 与圆 与圆 无公共点 无公共点 |
C.若圆 上存在两点关于直线 上存在两点关于直线 对称,则 对称,则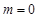 |
D.若直线 与圆 与圆 相交于 相交于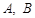 两点,则 两点,则 的最小值是 的最小值是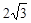 |
D
解析试题分析:由 :
: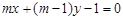 得:
得: ,所以过定点
,所以过定点 ,选项A错。又定点
,选项A错。又定点 与圆心的距离为1小于半径2,所以定点在圆内,所以选项B错。若圆
与圆心的距离为1小于半径2,所以定点在圆内,所以选项B错。若圆 上存在两点关于直线
上存在两点关于直线 对称,则直线过圆心,求得m=1,所以选项C错。当定点为AB中点时,线段AB最短,求得
对称,则直线过圆心,求得m=1,所以选项C错。当定点为AB中点时,线段AB最短,求得 的最小值是
的最小值是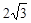 ,所以选项D对。
,所以选项D对。
考点:本题考查直线系方程、圆的一般式方程以及直线与圆的位置关系。
点评:直线系过定点的求法要当心,一般转化为 这种形式,联立
这种形式,联立 求解即为定点。
求解即为定点。

练习册系列答案
相关题目
已知直线的倾斜角为45°,在y轴上的截距为2,则此直线方程为( )
A. . . | B. |
C. | D. |
过点(1,0)且与直线 平行的直线方程是( )
平行的直线方程是( )
A. | B. |
C. | D. |
已知点 在直线
在直线 上,则
上,则 的最小值是( )
的最小值是( )
| A.4 | B.6 | C.8 | D.9 |
(文科) 两条直线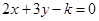 和
和 的交点在
的交点在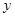 轴上,那么
轴上,那么 的值是 ( )
的值是 ( )
| A.-24 | B.6 | C.±6 | D.24 |
已知直线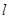 垂直于直线
垂直于直线 ,则直线
,则直线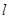 的斜率为( )
的斜率为( )
A. | B. | C.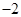 | D.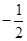 |
直线与函数 的图像相切于点
的图像相切于点 ,且
,且 ,
, 为坐标原点,
为坐标原点, 为图像的极大值点,与
为图像的极大值点,与 轴交于点
轴交于点 ,过切点
,过切点 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,则
,则 =
=
A. | B. | C. | D. 2 |
若 满足
满足 , 则直线
, 则直线 过定点 ( )
过定点 ( )
A. | B. | C. | D. |
设直线 的倾斜角为
的倾斜角为 ,且sin
,且sin +cos
+cos =0,则
=0,则 满足( )
满足( )
A. | B. | C. | D. |