题目内容
在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为 .过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
.过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
(1)求椭圆C的方程;
(2)设直线l1的斜率k>0,在x轴上是否存在点P(m,0),使得以PG,PH为邻边的平行四边形为菱形?如果存在,求出m的取值范围;如果不存在,请说明理由.
 .过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
.过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).(1)求椭圆C的方程;
(2)设直线l1的斜率k>0,在x轴上是否存在点P(m,0),使得以PG,PH为邻边的平行四边形为菱形?如果存在,求出m的取值范围;如果不存在,请说明理由.
(1)  =1(2)
=1(2)
 =1(2)
=1(2)
(1)设椭圆的方程为 =1(a>b>0),由离心率e=
=1(a>b>0),由离心率e= =
= ,△ABF2的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=8,得a=2,c=1,则b2=a2-c2=3.
,△ABF2的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=8,得a=2,c=1,则b2=a2-c2=3.
所以椭圆C的方程为 =1.
=1.
(2)由题意可知,直线l1的方程为y=kx+3(k>0).
由 得(3+4k2)x2+24kx+24=0,①
得(3+4k2)x2+24kx+24=0,①
Δ=(24k)2-4×24×(3+4k2)>0,解得k> .
.
设椭圆的弦GH的中点为N(x0,y0),则“在x轴上是否存在点P(m,0),使得以PG,PH为邻边的平行四边形为菱形”等价于“在x轴上是否存在点P(m,0),使得PN⊥l1”.
设G(x1,y1),H(x2,y2),由韦达定理,得x1+x2=- ,
,
则x0= =-
=- ,所以y0=kx0+3=
,所以y0=kx0+3= ,
,
即N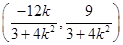 ,kPN=-
,kPN=-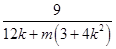 .
.
从而-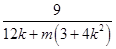 ·k=-1,
·k=-1,
解得m=-
 .
.
又因为m′(k)=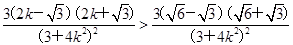 >0,
>0,
所以函数m=- 在定义域
在定义域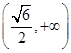 上单调递增,且mmin=m
上单调递增,且mmin=m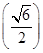 =-
=- ,即m∈
,即m∈ .
.
故存在满足条件的点P(m,0),m的取值范围为
 =1(a>b>0),由离心率e=
=1(a>b>0),由离心率e= =
= ,△ABF2的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=8,得a=2,c=1,则b2=a2-c2=3.
,△ABF2的周长为|AF1|+|AF2|+|BF1|+|BF2|=4a=8,得a=2,c=1,则b2=a2-c2=3.所以椭圆C的方程为
 =1.
=1.(2)由题意可知,直线l1的方程为y=kx+3(k>0).
由
 得(3+4k2)x2+24kx+24=0,①
得(3+4k2)x2+24kx+24=0,①Δ=(24k)2-4×24×(3+4k2)>0,解得k>
 .
.设椭圆的弦GH的中点为N(x0,y0),则“在x轴上是否存在点P(m,0),使得以PG,PH为邻边的平行四边形为菱形”等价于“在x轴上是否存在点P(m,0),使得PN⊥l1”.
设G(x1,y1),H(x2,y2),由韦达定理,得x1+x2=-
 ,
,则x0=
 =-
=- ,所以y0=kx0+3=
,所以y0=kx0+3= ,
,即N
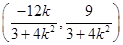 ,kPN=-
,kPN=-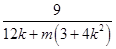 .
.从而-
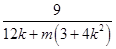 ·k=-1,
·k=-1,解得m=-

 .
.又因为m′(k)=
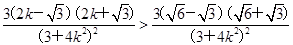 >0,
>0,所以函数m=-
 在定义域
在定义域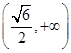 上单调递增,且mmin=m
上单调递增,且mmin=m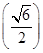 =-
=- ,即m∈
,即m∈ .
.故存在满足条件的点P(m,0),m的取值范围为


练习册系列答案
相关题目
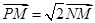 .
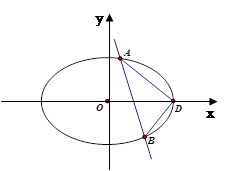
.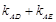 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.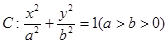 过点
过点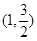 ,且离心率
,且离心率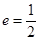 .
.
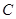 的标准方程;
的标准方程;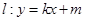 与椭圆
与椭圆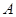 ,
,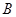 两点(
两点(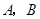 不是左右顶点),椭圆的右顶点为
不是左右顶点),椭圆的右顶点为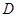 ,且满足
,且满足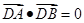 ,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由. 的中心在坐标原点O,左顶点
的中心在坐标原点O,左顶点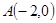 ,离心率
,离心率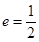 ,
,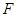 为右焦点,过焦点
为右焦点,过焦点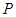 、
、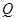 两点(不同于点
两点(不同于点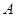 ).
).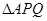 的面积
的面积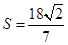 时,求直线PQ的方程;
时,求直线PQ的方程;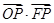 的范围.
的范围. +
+ =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 .
. ·
· +
+ ·
· =8,求k的值.
=8,求k的值. +
+ =1恒有公共点,则实数m的取值范围是( )
=1恒有公共点,则实数m的取值范围是( ) =1与双曲线C2:
=1与双曲线C2: =1共焦点,则椭圆C1的离心率e的取值范围为( )
=1共焦点,则椭圆C1的离心率e的取值范围为( )


 =1的左焦点为F1,右顶点为A,上顶点为B.若∠F1BA=90°,则椭圆的离心率是( )
=1的左焦点为F1,右顶点为A,上顶点为B.若∠F1BA=90°,则椭圆的离心率是( ) B.
B. C.
C. D.
D.


 ,+∞
,+∞