题目内容
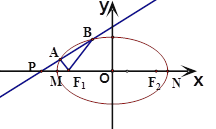
已知椭圆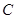 的中心在坐标原点O,左顶点
的中心在坐标原点O,左顶点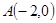 ,离心率
,离心率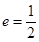 ,
,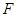 为右焦点,过焦点
为右焦点,过焦点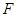 的直线交椭圆
的直线交椭圆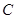 于
于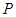 、
、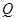 两点(不同于点
两点(不同于点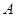 ).
).
(1)求椭圆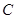 的方程;
的方程;
(2)当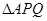 的面积
的面积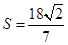 时,求直线PQ的方程;
时,求直线PQ的方程;
(3)求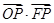 的范围.
的范围.
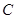 的中心在坐标原点O,左顶点
的中心在坐标原点O,左顶点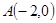 ,离心率
,离心率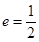 ,
,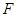 为右焦点,过焦点
为右焦点,过焦点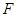 的直线交椭圆
的直线交椭圆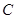 于
于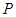 、
、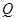 两点(不同于点
两点(不同于点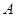 ).
).(1)求椭圆
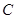 的方程;
的方程;(2)当
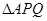 的面积
的面积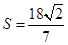 时,求直线PQ的方程;
时,求直线PQ的方程;(3)求
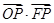 的范围.
的范围.(1)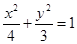 ;(2)
;(2)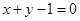 或
或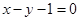 ;(3)(2,6)
;(3)(2,6)
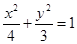 ;(2)
;(2)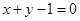 或
或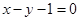 ;(3)(2,6)
;(3)(2,6)试题分析:(1)设出椭圆的标准方程根据题意可a,利用离心率求得c,则b可求得,椭圆的方程可得.
(2)设出直线PQ的方程,与椭圆方程联立,设出P,Q的坐标,进而根据韦达定理表示出
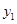
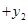 和
和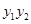 ,则利用弦长公式可表示出|PQ|,进而可表示出
,则利用弦长公式可表示出|PQ|,进而可表示出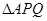 的面积方程可得.
的面积方程可得.(3)利用向量的坐标运算,建立函数关系式,利用椭圆的范围找到定义域,利用二次函数即可求范围.
试题解析:(1)设椭圆方程为
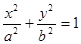 (a>b>0) ,由已知
(a>b>0) ,由已知 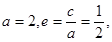
∴
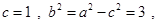 2分
2分∴ 椭圆方程为
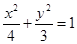 . 4分
. 4分(2)解法一: 椭圆右焦点
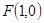 . 设直线
. 设直线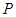
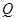 方程为
方程为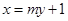 (
(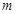 ∈R). 5分
∈R). 5分由
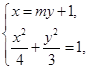 得
得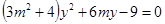 .① 6分
.① 6分显然,方程①的
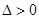 .设
.设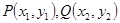 ,则有
,则有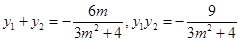 . 8分
. 8分由
 的面积
的面积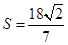 =
=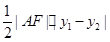 =
=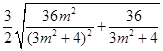
解得:
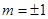 .
.∴直线PQ 方程为
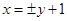 ,即
,即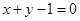 或
或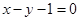 . 10分
. 10分解法二:
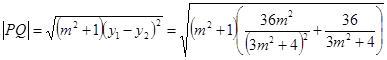
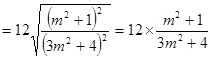 . 6分
. 6分点A到直线PQ的距离
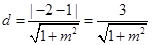 8分
8分由
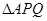 的面积
的面积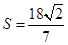 =
=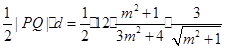 解得
解得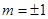 .
.∴直线PQ 方程为
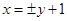 ,即
,即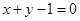 或
或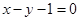 . 10分
. 10分解法三: 椭圆右焦点
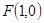 .当直线的斜率不存在时,
.当直线的斜率不存在时,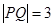 ,不合题意. 5分
,不合题意. 5分当直线的斜率存在时,设直线
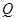 方程为
方程为 ,
, 由
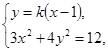 得
得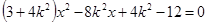 . ① 6分
. ① 6分显然,方程①的
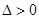 .
.设
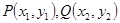 ,则
,则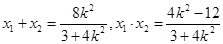 . 7分
. 7分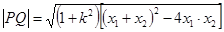
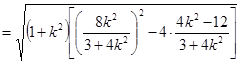
=
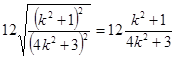 . 8分
. 8分点A到直线PQ的距离
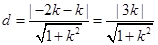 9分
9分由
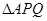 的面积
的面积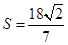 =
=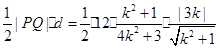 解得
解得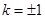 .
.∴直线
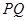 的方程为
的方程为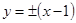 ,即
,即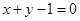 或
或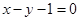 . 10分
. 10分(3)设P的坐标(
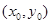 则
则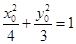 ∴
∴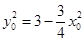
故
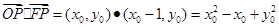
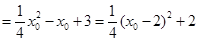 12分
12分∵
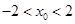 ∴
∴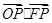 的范围为(2,6) 14分
的范围为(2,6) 14分(注:以上解答题其他解法相应给分)

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
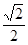 的椭圆
的椭圆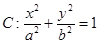 (
(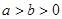 )过点
)过点
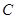 的方程;
的方程;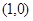 作斜率为
作斜率为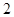 直线
直线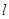 与椭圆相交于
与椭圆相交于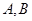 两点,求
两点,求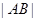 的长.
的长. :
: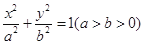 的左焦点为
的左焦点为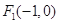 ,且过点
,且过点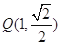 .
.
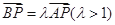 .
.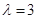 ,求
,求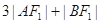 的值;
的值;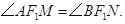
 .过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).
.过F1的直线交椭圆C于A,B两点,且△ABF2的周长为8.过定点M(0,3)的直线l1与椭圆C交于G,H两点(点G在点M,H之间).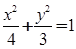 上运动,Q、R分别在两圆
上运动,Q、R分别在两圆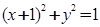 和
和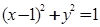 上运动,则
上运动,则 的最小值为
的最小值为 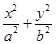 =1(a>b>0)恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.
=1(a>b>0)恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.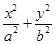 =1(a>b>0)的一个焦点和一个顶点,则该椭圆的离心率为________.
=1(a>b>0)的一个焦点和一个顶点,则该椭圆的离心率为________.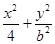 =1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为( ).
=1(0<b<2)与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为( ).


