题目内容

甲、乙等五名工人被随机地分到A，B，C三个不同的岗位工作，每个岗位至少有一名工人．
（1）求甲、乙被同时安排在A岗位的概率；
（2）设随机变量ξ为这五名工人中参加A岗位的人数，求ξ的分布列和数学期望．

解：（1）五名工人被随机地分到A，B，C三个不同的岗位工作，每个岗位至少有一名工人，
可以有一个岗位3人，其余各1人，有 $\text{[math]}$ 种，也可能有一个岗位1人，其余各2人，有3 $\text{[math]}$ 种，
要满足甲、乙被同时安排在A岗位，则相当于把其余3人分到A，B，C岗位，有 $\text{[math]}$ 种，
故所求的概率为： $\text{[math]}$ ；（6分）
（2）ξ可以取1，2，3 同（1）的求法可得 $\text{[math]}$ （8分）
$\text{[math]}$ （10分）
$\text{[math]}$ （12分）
∴ξ的分布列为：

ξ	1	2	3
P	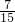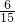$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

故 $\text{[math]}$ （14分）
分析：（1）由分类和分步计数原理可得总的基本事件为 $\text{[math]}$ + $\text{[math]}$ ，符合条件的有 $\text{[math]}$ 种，由古典概型的公式可得答案；
（2）ξ可以取1，2，3分别可得其对应的概率，即得分布列，由期望的定义可得期望值．
点评：本题考查离散型随机变量及其分布列，涉及数学期望，属中档题．