Question

【题目】如图，在三棱柱A1B1C1﹣A2B2C2中，各侧棱均垂直于底面，∠A1B1C1=90°，A1B1=B1C1=3，C1M=2B1N=2，则直线B1C1与平面A1MN所成角的正弦值为 ．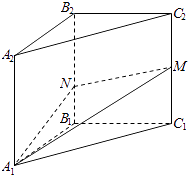

Answer 1

【答案】
【解析】解：∵在三棱柱A1B1C1﹣A2B2C2中，各侧棱均垂直于底面，∠A1B1C1=90°，A1B1=B1C1=3，C1M=2B1N=2，
∴以B1为原点，B1A1为x轴，B1C1为y轴，B1B2为z轴，建立空间直角坐标系，
则B1（0，0，0），C1（0，3，0），A1（3，0，0），N（0，0，1），M（0，3，2），
=（0，3，0）， =（3，0，﹣1）， =（0，3，1），
设平面NA1M的法向量 =（x，y，z），
则 ，取x=1得 =（1，﹣1，3），
设直线B1C1与平面A1MN所成角为θ，
则sinθ= = = ．
∴直线B1C1与平面A1MN所成角的正弦值为 ．
所以答案是： ．

【考点精析】掌握空间角的异面直线所成的角是解答本题的根本，需要知道已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则．