题目内容
已知椭圆E：| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
（1）求椭圆E的标准方程；
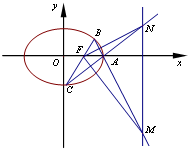
（2）若经过F的直线l（不与x轴重合）交椭圆E与B，C两点，延长BA，CA，分别交右准线于M，N两点．求证：FN⊥FM．
分析：（1）利用椭圆E：
+
=1(a＞b＞0)过点P （1，
），离心率e=
，确定椭圆的几何量，即可求椭圆E的标准方程；
（2）分类讨论，确定直线BA、CA的方程，求出M、N的坐标，利用验证向量的数量积为0，即可证得结论．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
（2）分类讨论，确定直线BA、CA的方程，求出M、N的坐标，利用验证向量的数量积为0，即可证得结论．
解答：（1）解：由题意，∵椭圆E：
+
=1(a＞b＞0)过点P （1，
），离心率e=
，
∴
+
=1，
=
∵a2=b2+c2
∴a2=4，b2=3
∴椭圆E的标准方程为
+
=1．…（4分）
（2）证明：由（1）知，A（2，0），F（1，0），右准线方程为x=4．
当直线l与x轴垂直时，l方程为x=1，可得B，C两点坐标分别为(1，
)，(1，-
)．
所以直线BA方程为
=
，当x=4时，得y=-3，即M（4，-3）；
直线CA方程为
=
，当x=4时，得y=3，即N（4，3）．
因此
=(3，-3)，
=(3，3)
∴
•
=3×3+(-3)×3=0，即FN⊥FM．…（8分）
当直线l与x轴不垂直时，设其方程为y=k（x-1）（k≠0）．
由题意得
，解之得x=
，代入直线l方程得
B（
，
），C（
，
）．…（10分）
直线BA方程为
=
，
当x=4时，得M（4，
），所以
=（3，
）．…（12分）
同理可求得
=（3，
）． …（14分）
∴
•
=9+
•
=9+
=0，
∴FN⊥FM．
综上，对于任意与x轴不重合的直线l，都有FN⊥FM．…（16分）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| a2 |
| 9 |
| 4b2 |
| c |
| a |
| 1 |
| 2 |
∵a2=b2+c2
∴a2=4，b2=3
∴椭圆E的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
（2）证明：由（1）知，A（2，0），F（1，0），右准线方程为x=4．
当直线l与x轴垂直时，l方程为x=1，可得B，C两点坐标分别为(1，
| 3 |
| 2 |
| 3 |
| 2 |
所以直线BA方程为
| y-0 | ||
|
| x-2 |
| 1-2 |
直线CA方程为
| y-0 | ||
-
|
| x-2 |
| 1-2 |
因此
| FM |
| FN |
∴
| FM |
| FN |
当直线l与x轴不垂直时，设其方程为y=k（x-1）（k≠0）．
由题意得
|
4k2±6
| ||
| 4k2+3 |
B（
4k2+6
| ||
| 4k2+3 |
6k
| ||
| 4k2+3 |
4k2-6
| ||
| 4k2+3 |
-6k
| ||
| 4k2+3 |
直线BA方程为
| y-0 | ||||
|
| x-2 | ||||
|
当x=4时，得M（4，
6k
| ||
3
|
| FM |
6k
| ||
3
|
同理可求得
| FN |
6k
| ||
3
|
∴
| FM |
| FN |
6k
| ||
3
|
6k
| ||
3
|
| 36k4+27k2 |
| -4k4-3k2 |
∴FN⊥FM．
综上，对于任意与x轴不重合的直线l，都有FN⊥FM．…（16分）
点评：本题考查椭圆的标准方程，考查直线的方程，考查向量知识的运用，考查分类讨论的数学思想，考查学生的综合能力，难度较大．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
（2012•佛山二模）已知椭圆E：