题目内容
已知数列 ,如果数列
,如果数列 满足
满足 ,
, ,其中
,其中 ,则称
,则称 为
为 的“生成数列”.
的“生成数列”.
(1)若数列 的
的 ,求
,求 ;
;
(2)若 为偶数,且
为偶数,且 的“生成数列”是
的“生成数列”是 ,证明:
,证明: 的“生成数列”是
的“生成数列”是 ;
;
(3)若 为奇数,且
为奇数,且 的“生成数列”是
的“生成数列”是 ,
, 的“生成数列”是
的“生成数列”是 ,…,依次将数列
,…,依次将数列 ,
, ,
, ,…的第
,…的第 项取出,构成数列
项取出,构成数列 …,证明:
…,证明: 是等差数列.
是等差数列.
 ,如果数列
,如果数列 满足
满足 ,
, ,其中
,其中 ,则称
,则称 为
为 的“生成数列”.
的“生成数列”.(1)若数列
 的
的 ,求
,求 ;
;(2)若
 为偶数,且
为偶数,且 的“生成数列”是
的“生成数列”是 ,证明:
,证明: 的“生成数列”是
的“生成数列”是 ;
;(3)若
 为奇数,且
为奇数,且 的“生成数列”是
的“生成数列”是 ,
, 的“生成数列”是
的“生成数列”是 ,…,依次将数列
,…,依次将数列 ,
, ,
, ,…的第
,…的第 项取出,构成数列
项取出,构成数列 …,证明:
…,证明: 是等差数列.
是等差数列.解:(1)由题意得: ;
; ;
;
 ;
;
 .
.
(2)因为 ,
,  ,
,  ,
,
 ,
,
由于 为偶数,将上述
为偶数,将上述 个等式中的第2,4,6,…,n这
个等式中的第2,4,6,…,n这 个式子都乘以
个式子都乘以 ,
,
相加得 …
… …
…
即 ,
, .
.
由于 ,
,
 ,
,
根据“生成数列”的定义知,数列 是
是 的” “生成数列”
的” “生成数列”
(3)证明:设数列 ,
, ,
, 中后者是前者的“生成数列”.
中后者是前者的“生成数列”.
欲证 成等差数列,只需证明
成等差数列,只需证明 成等差数列,
成等差数列,
即只要证明
 即可.
即可.
由(2)中结论可知 ,
,




 ,
,
所以, ,即
,即 成等差数列,
成等差数列,
所以 是等差数列.
是等差数列.
 ;
; ;
; ;
;
 .
. (2)因为
 ,
,  ,
,  ,
, ,
, 由于
 为偶数,将上述
为偶数,将上述 个等式中的第2,4,6,…,n这
个等式中的第2,4,6,…,n这 个式子都乘以
个式子都乘以 ,
,相加得
 …
… …
…
即
 ,
, .
. 由于
 ,
,
 ,
,根据“生成数列”的定义知,数列
 是
是 的” “生成数列”
的” “生成数列” (3)证明:设数列
 ,
, ,
, 中后者是前者的“生成数列”.
中后者是前者的“生成数列”.欲证
 成等差数列,只需证明
成等差数列,只需证明 成等差数列,
成等差数列,即只要证明

 即可.
即可. 由(2)中结论可知
 ,
,



 ,
,所以,
 ,即
,即 成等差数列,
成等差数列,所以
 是等差数列.
是等差数列. 
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
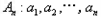 ,如果数列
,如果数列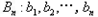 满足
满足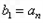 ,
,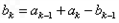 ,其中
,其中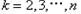 ,则称
,则称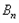 为
为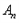 的“生成数列”.
的“生成数列”. 的“生成数列”是
的“生成数列”是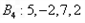 ,求
,求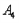 ;
;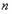 为偶数,且
为偶数,且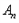 的“生成数列”是
的“生成数列”是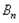 ,证明:
,证明: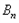 的“生成数列”是
的“生成数列”是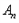 ;
;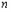 为奇数,且
为奇数,且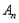 的“生成数列”是
的“生成数列”是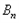 ,
,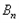 的“生成数列”是
的“生成数列”是 ,….依次将数列
,….依次将数列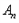 ,
,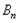 ,
,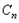 ,…的第
,…的第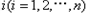 项取出,构成数列
项取出,构成数列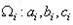 ,…,探究:数列
,…,探究:数列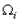 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.