题目内容
(12分)定义在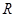 上的函数
上的函数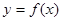 ,
,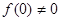 ,当
,当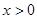 时,
时,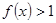 .且对任意的
.且对任意的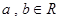 有
有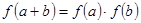 。
。
(1)证明: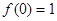 ;
;
(2)证明:对任意的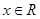 ,恒有
,恒有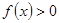 ;
;
(3)证明: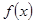 是
是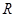 上的增函数;
上的增函数;
(4)若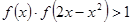 ,求
,求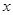 的取值范围。
的取值范围。
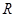 上的函数
上的函数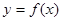 ,
,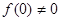 ,当
,当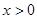 时,
时,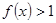 .且对任意的
.且对任意的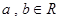 有
有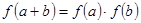 。
。(1)证明:
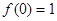 ;
;(2)证明:对任意的
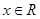 ,恒有
,恒有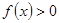 ;
;(3)证明:
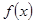 是
是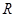 上的增函数;
上的增函数;(4)若
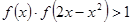 ,求
,求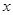 的取值范围。
的取值范围。(1)令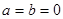 即可证明(2)分
即可证明(2)分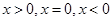 证明即可
证明即可
(3)利用单调性定义即可证明(4)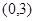
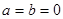 即可证明(2)分
即可证明(2)分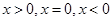 证明即可
证明即可(3)利用单调性定义即可证明(4)
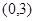
试题分析:(1)证明:令
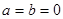 ,
,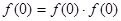 ,又
,又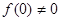 ,
,所以
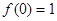 . ……2分
. ……2分(2)证明:由已知当
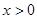 时,
时,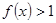 ,由(1)得
,由(1)得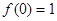 ,
,故当
 时,
时,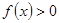 成立,
成立,当
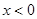 时,
时,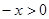 ,所以
,所以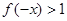 ,
,而
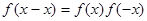 ,所以
,所以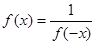 ,
,可得
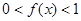
综上:对任意的
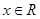 ,恒有
,恒有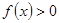 成立. ……6分
成立. ……6分(3)证明:设
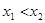 ,则
,则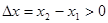 ,
,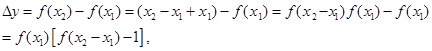
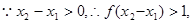 而
而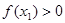 ,
,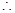
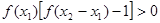 ,
,即
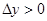 ,
,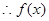 是
是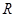 上增函数得证。 ……10分
上增函数得证。 ……10分(4)由
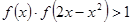 ,可得
,可得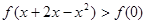 ,
,又因为
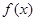 是
是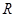 上增函数,所以
上增函数,所以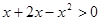 ,解得
,解得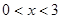 ,
,所以:所求
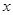 的取值范围
的取值范围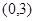 . ……12分
. ……12分点评:求解抽象函数问题,主要的方法是赋值法,证明抽象函数的单调性只能用定义,证明时要尽量化简到最简单.

练习册系列答案
相关题目
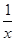 -2(x<0),则f(x)的最大值为
-2(x<0),则f(x)的最大值为 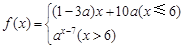 若数列{an}满足an=
若数列{an}满足an=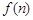 (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( )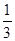 ,1)
,1)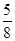 )
)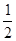 )
)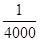 ).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=
).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=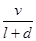 最大?
最大?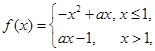 若
若 ,
,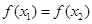 成立,则实数
成立,则实数 的取值范围是 。
的取值范围是 。
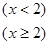 则
则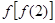 =( )
=( )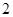
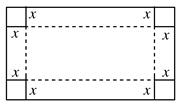
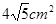 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽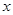 及长
及长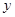 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.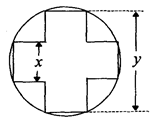
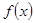 在
在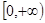 上是增函数,
上是增函数, 若
若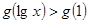 ,则
,则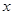 的取值范围是( )
的取值范围是( )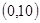
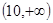

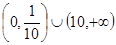
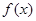 ,并指出函数
,并指出函数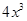 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值.