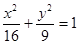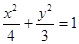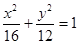题目内容
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B.(1,0) | C.(0,- ) ) | D.(- ,0) ,0) |
C
解析试题分析:因为抛物线 ,那么可知2p=
,那么可知2p=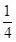 ,焦点在y轴上,开口向下,那么焦点坐标为(0,-
,焦点在y轴上,开口向下,那么焦点坐标为(0,- )故选C.
)故选C.
考点:本题主要考查了抛物线的几何性质.
点评:解决该试题的关键是将抛物线方程化为标准方程,确定抛物线的开口方向与对称轴.进而得到结论。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
已知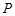 是椭圆
是椭圆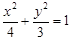 上的一点,
上的一点,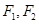 是该椭圆的两个焦点,若
是该椭圆的两个焦点,若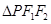 的内切圆半径为
的内切圆半径为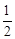 ,则
,则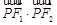 的值为( )
的值为( )
A.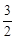 | B.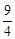 | C.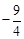 | D. 0 |
设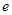 是椭圆
是椭圆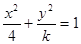 的离心率,且
的离心率,且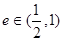 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
| A. (0,3) | B. (3,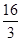 ) ) |
C. (0,3)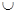 ( ( 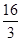 ,+ ,+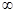 ) ) | D. (0,2) |
从双曲线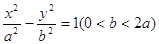 的左焦点
的左焦点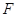 引圆
引圆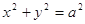 的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则
的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则 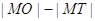 与
与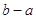 的大小关系为
的大小关系为 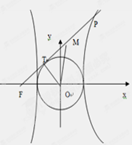
A.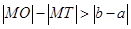 |
B.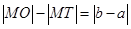 |
C.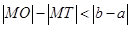 |
| D.不能确定 |
若双曲线 的左焦点在抛物线
的左焦点在抛物线 的准线上,则
的准线上,则 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
到两定点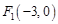 、
、 的距离之差的绝对值等于6的点
的距离之差的绝对值等于6的点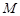 的轨迹
的轨迹
| A.椭圆 | B.线段 | C.双曲线 | D.两条射线 |
动点 到点
到点 及点
及点 的距离之差为2,则点
的距离之差为2,则点 的轨迹是
的轨迹是
| A.双曲线 | B.双曲线的一支 | C.两条射线 | D.一条射线 |
椭圆 上一点
上一点 到焦点
到焦点 的距离为2,
的距离为2, 是
是 的中点,则
的中点,则 等于( )
等于( )
| A.2 | B. | C. | D. |