题目内容
已知在△ABC中,内角A,B,C所对的边分别为a,b,c,且 .
.
(Ⅰ)求角A;
(Ⅱ)若a=l,且 ,求角B.
,求角B.
解:(Ⅰ)由 ,可得sinAcosC+
,可得sinAcosC+ sinC=sinB.
sinC=sinB.
而sinB=sin(A+C)=sinAcosC+cosAsinC.
可得 sinC=cosAsinC,sinC≠0,
sinC=cosAsinC,sinC≠0,
所以 =cosA,A∈(0,π),所以A=
=cosA,A∈(0,π),所以A= ;
;
(Ⅱ)因为a=l,由 ,即
,即 ,
,
由正弦定理得 sinC-2sinB=sinA,
sinC-2sinB=sinA,
∵A=
C= ,∴
,∴ sin(
sin( )-2sinB=
)-2sinB= ,
,
整理得cos(B+ )=
)= ,
,
∵ ,∴B+
,∴B+ ∈
∈
∴B+ =
= ,
,
所以B= .
.
分析:(Ⅰ)通过已知表达式,利用正弦定理,以及三角形的内角和,转化sinB=sin(A+C),通过两角和的正弦函数,化简可求A的余弦值,即可求角A;
(Ⅱ)利用a=l,以及 ,通过正弦定理,三角形的内角和,转化方程只有B的三角方程,结合B的范围,求角B.
,通过正弦定理,三角形的内角和,转化方程只有B的三角方程,结合B的范围,求角B.
点评:本题考查正弦定理与两角和的正弦函数的应用,三角形的内角和以及三角函数值的求法,考查计算能力.
 ,可得sinAcosC+
,可得sinAcosC+ sinC=sinB.
sinC=sinB.而sinB=sin(A+C)=sinAcosC+cosAsinC.
可得
 sinC=cosAsinC,sinC≠0,
sinC=cosAsinC,sinC≠0,所以
 =cosA,A∈(0,π),所以A=
=cosA,A∈(0,π),所以A= ;
;(Ⅱ)因为a=l,由
 ,即
,即 ,
,由正弦定理得
 sinC-2sinB=sinA,
sinC-2sinB=sinA,∵A=

C=
 ,∴
,∴ sin(
sin( )-2sinB=
)-2sinB= ,
,整理得cos(B+
 )=
)= ,
,∵
 ,∴B+
,∴B+ ∈
∈
∴B+
 =
= ,
,所以B=
 .
.分析:(Ⅰ)通过已知表达式,利用正弦定理,以及三角形的内角和,转化sinB=sin(A+C),通过两角和的正弦函数,化简可求A的余弦值,即可求角A;
(Ⅱ)利用a=l,以及
 ,通过正弦定理,三角形的内角和,转化方程只有B的三角方程,结合B的范围,求角B.
,通过正弦定理,三角形的内角和,转化方程只有B的三角方程,结合B的范围,求角B.点评:本题考查正弦定理与两角和的正弦函数的应用,三角形的内角和以及三角函数值的求法,考查计算能力.

练习册系列答案
相关题目
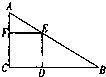 如图所示,已知在△ABC中,∠C=90°,正方形DEFC内接于△ABC,DE∥AC,EF∥BC,AC=1,BC=2,则AF:FC=
如图所示,已知在△ABC中,∠C=90°,正方形DEFC内接于△ABC,DE∥AC,EF∥BC,AC=1,BC=2,则AF:FC=