题目内容
(2012•安徽模拟)已知集合A={x|x2-3x≤0},B={y|y=-x2+2,x∈[-2,-1]},则A∩B=( )
分析:求出集合A中一元二次不等式的解集,确定出集合A,由集合B中的函数为二次函数,根据二次函数的值域确定出集合B,把两集合的解集表示在数轴上,找出两解集的公共部分即可得到两集合的交集.
解答:解:由集合B中的函数y=-x2+2,x∈[-2,-1],得到集合B=[-2,1],
由集合A中的不等式x2-3x≤0,因式分解得x(x-3)≤0,
解得:0≤x≤3,得到集合A=[0,3],
把两集合的解集画在数轴上,如图所示:
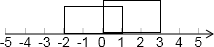
则A∩B=[0,1].
故选B.
由集合A中的不等式x2-3x≤0,因式分解得x(x-3)≤0,
解得:0≤x≤3,得到集合A=[0,3],
把两集合的解集画在数轴上,如图所示:

则A∩B=[0,1].
故选B.
点评:此题属于以函数的值域及一元二次不等式的解法为平台,考查了交集的运算,是高考中常考的基本题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目