题目内容
设函数
为偶函数，则
（ ）
| A．1 | B． | C．0 | D．2 |
B
解析试题分析：因为函数为偶函数，所以
，整理得，
=0，所以，故选B。
考点：本题主要考查函数的奇偶性。
点评：简单题，利用函数奇偶性定义加以研究。
练习册系列答案
相关题目
为了求函数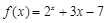
的一个零点，某同学利用计算器得到自变量
和函数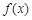
的部分对应值，如表所示：
| 1.25 | 1.3125 | 1.375 | 1.4375 | 1.5 | 1.5625 |
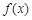| －0.8716 | －0.5788 | －0.2813 | 0.2101 | 0.32843 | 0.64115 |
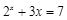的近似解（精确到0.1）可取为（A）1.32 （B）1.39 （C）1.4 （D）1.3
对于函数f (x)和g(x)，其定义域为[a, b]，若对任意的x∈[a, b]总有|1－
|≤
，则称f (x)可被g(x)置换，那么下列给出的函数中能置换f (x)=
x∈[4，16]的是 ( )
| A．g(x)=2x+6 x∈[4，16] | B．g(x)=x2+9 x∈[4，16] |
C．g(x)=  (x+8) x∈[4，16] | D．g(x)= (x+6) x∈[4，16] |
下列说法正确的是
A．函数 在其定义域上是减函数 |
| B．两个三角形全等是这两个三角形面积相等的必要条件 |
C．命题“ R， ”的否定是“  R， ” |
D．给定命题 、 ，若 是真命题，则 是假命题 |
下列函数中既是偶函数又在
（ ）
A． | B． | C． | D． |
若函数
是奇函数，则
＝（ ）
| A．１ | B．０ | C．２ | D．－１ |
已知
为定义在
上的可导函数，且
对于
恒成立，则（ ）
A． |
B． |
C． |
D． |
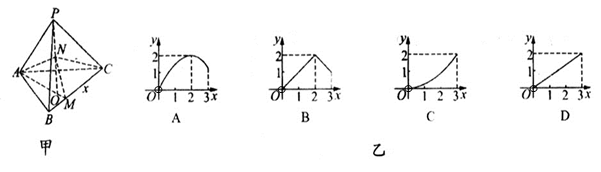
的高
，
，
，M、N分别在
和
上，且
，
，图乙中的四个图像大致描绘了三棱锥
的体积V与
的变化关系，其中正确的是（ ）