题目内容
下列说法正确的是
A.函数 在其定义域上是减函数 在其定义域上是减函数 |
| B.两个三角形全等是这两个三角形面积相等的必要条件 |
C.命题“ R, R, ”的否定是“ ”的否定是“  R, R, ” ” |
D.给定命题 、 、 ,若 ,若 是真命题,则 是真命题,则 是假命题 是假命题 |
D
解析试题分析:函数 在
在 和
和 上都单调递减,但是在定义域上不是减函数,所以A不正确;两个三角形全等是这两个三角形面积相等的充分不必要条件,所以B不正确;“
上都单调递减,但是在定义域上不是减函数,所以A不正确;两个三角形全等是这两个三角形面积相等的充分不必要条件,所以B不正确;“ ”的否定是“
”的否定是“ ”,所以C不正确;根据复合命题的真值表,可以判定出C正确.
”,所以C不正确;根据复合命题的真值表,可以判定出C正确.
考点:本小题主要考查函数单调性的考查、充分条件和必要条件的判断、特称命题的否定和复合命题真假的判断,考查学生的逻辑推理能力.
点评:函数的单调性是一个区间概念,一个函数可能有几个单调区间,但是在定义域上并不是单调函数;判断充分条件和必要条件,要分清条件和结论,分清由谁能推出谁.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
如果偶函数 ,当
,当 时,
时,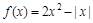 ,则
,则 在
在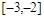 上是( )
上是( )
A.增函数,最大值为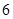 | B.增函数,最小值是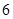 |
C.减函数,最大值为 | D.减函数,最小值是 |
函数 的零点个数
的零点个数
| A.0 | B.1 |
| C.2 | D.1或2 |
下列函数是偶函数的是( )
A.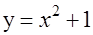 , ,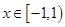 | B.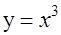 |
C. | D. |
下列函数中,在区间 上是增函数的是 ( )
上是增函数的是 ( )
A. | B. | C. | D. |
已知函数 的定义域为( )
的定义域为( )
A. | B. |
C. | D. |
设函数 为偶函数,则
为偶函数,则 ( )
( )
| A.1 | B. | C.0 | D.2 |
函数 的定义域为 ( )
的定义域为 ( )
| A.(e,+∞) | B.[e,+∞) | C. (O,e] | D.(-∞,e] |
 的定义域为
的定义域为 ,值域为
,值域为 ,则点
,则点 表示的图形可以是( )
表示的图形可以是( ) 