题目内容
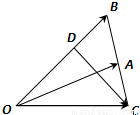
 已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设
已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设| OA |
| a |
| OB |
| b |
(1)用
| a |
| b |
| OC |
| DC |
(2)若向量
| OC |
| OA |
| DC |
分析:(1)由A是BC中点,得
=
(
+
),从而算出
=2
-
,再由向量减法法则即可得到
=2
-
;
(2)根据(1)的结论,可得
+k
关于向量
,
的表示式,而
=2
-
,结合向量共线的充要条件建立关于k的方程组,解之即可得到实数k的值.
| OA |
| 1 |
| 2 |
| OB |
| OC |
| OC |
| a |
| b |
| DC |
| a |
| 5 |
| 3 |
| b |
(2)根据(1)的结论,可得
| OA |
| DC |
| a |
| b |
| OC |
| a |
| b |
解答:解:(1)∵A为BC的中点,∴
=
(
+
),
可得
=2
-
=2
-
,
而
=
-
=
-
=2
-
(2)由(1),得
+k
=(2k+1)
-
k
,
∵
与
+k
共线,设
=λ(
+k
)
即2
-
=λ(2k+1)
+-
λk
,
根据平面向量基本定理,得
解之得,k=
.
| OA |
| 1 |
| 2 |
| OB |
| OC |
可得
| OC |
| OA |
| OB |
| a |
| b |
而
| DC |
| OC |
| OD |
| OC |
| 2 |
| 3 |
| OB |
| a |
| 5 |
| 3 |
| b |
(2)由(1),得
| OA |
| DC |
| a |
| 5 |
| 3 |
| b |
∵
| OC |
| OA |
| DC |
| OC |
| OA |
| DC |
即2
| a |
| b |
| a |
| 5 |
| 3 |
| b |
根据平面向量基本定理,得
|
解之得,k=
| 3 |
| 4 |
点评:本题给出三角形中的向量,求向量的线性表示式并求实数k的值.着重考查了向量加减法的运算法则和平面向量共线的条件等知识,属于基础题.

练习册系列答案
相关题目
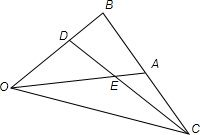 已知△OAB中,点C是点B关于点A的对称点,点D是线段OB的一个靠近B的三等分点,设
已知△OAB中,点C是点B关于点A的对称点,点D是线段OB的一个靠近B的三等分点,设 已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设
已知△OAB中,点D在线段OB上,且OD=2DB,延长BA到C,使BA=AC.设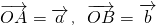 .
. 表示向量
表示向量 ;
; 与
与 共线,求k的值.
共线,求k的值.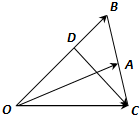
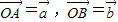 .
.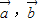 表示向量
表示向量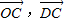 ;
;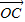 与
与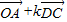 共线,求k的值.
共线,求k的值.