题目内容
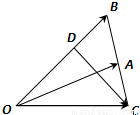
已知△OAB中，点D在线段OB上，且OD=2DB，延长BA到C，使BA=AC．设
=
，
=
．
（1）用
，
表示向量
，
；
（2）若向量
与
+k
共线，求k的值．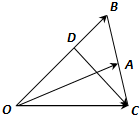
| OA |
| a |
| OB |
| b |
（1）用
| a |
| b |
| OC |
| DC |
（2）若向量
| OC |
| OA |
| DC |
（1）∵A为BC的中点，∴
=
(
+
)，
可得
=2
-
=2
-
，
而
=
-
=
-
=2
-
（2）由（1），得
+k
=(2k+1)
-
k
，
∵
与
+k
共线，设
=λ(
+k
)
即2
-
=λ(2k+1)
+-
λk
，
根据平面向量基本定理，得
解之得，k=
．
| OA |
| 1 |
| 2 |
| OB |
| OC |
可得
| OC |
| OA |
| OB |
| a |
| b |
而
| DC |
| OC |
| OD |
| OC |
| 2 |
| 3 |
| OB |
| a |
| 5 |
| 3 |
| b |
（2）由（1），得
| OA |
| DC |
| a |
| 5 |
| 3 |
| b |
∵
| OC |
| OA |
| DC |
| OC |
| OA |
| DC |
即2
| a |
| b |
| a |
| 5 |
| 3 |
| b |
根据平面向量基本定理，得
|
解之得，k=
| 3 |
| 4 |
练习册系列答案
相关题目
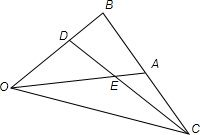已知△OAB中，点C是点B关于点A的对称点，点D是线段OB的一个靠近B的三等分点，设
已知△OAB中，点D在线段OB上，且OD=2DB，延长BA到C，使BA=AC．设
已知△OAB中，点D在线段OB上，且OD=2DB，延长BA到C，使BA=AC．设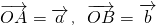
．
表示向量
；
与
共线，求k的值．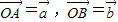
．
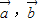表示向量
；
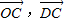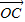与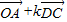
共线，求k的值．