题目内容
2002年底某县的绿化面积占全县总面积的40%，从2003年开始，计划每年将非绿化面积的8%绿化，由于修路和盖房等用地，原有绿化面积的2%被非绿化.(1)设该县的总面积为1，2002年底绿化面积为a1=
，经过n年后绿化的面积为an+1,试用an表示an+1;
(2)求数列{an}的第n+1项an+1;
(3)至少需要多少年的努力，才能使绿化率超过60%?(lg2=0.301 0,lg3=0.477 1)
解:(1)设现有非绿化面积为b1,经过n年后非绿化面积为bn+1.
于是a1+b1=1,an+bn=1.
依题意，an+1是由两部分组成，一部分是原有的绿化面积an减去被非绿化部分an后剩余的面积
an，另一部分是新绿化的面积
bn，于是
an+1=
an+
bn=
an+
(1-an)
=
an+
.
(2)an+1=
an+
,an+1-
=
(an-
).
数列{an-
}是公比为
,首项为a1-
=
-
=-
的等比数列.
∴an+1=
+(-
)(
)n.
(3)an+1＞60%,
+(-
)(
)n＞
,(
)n＜
,n(lg9-1)＜-lg2,n＞
≈6.572 0.
至少需要7年，绿化率才能超过60%.
练习册系列答案
相关题目
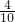，经过n年后绿化的面积为an+1，试用an表示an+1；
，经过n年后绿化的面积为an+1，试用an表示an+1；
，经过n年后绿化的面积为an+1，试用an表示an+1；