题目内容
已知函数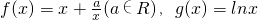 .
.
(1)求函数F(x)=f(x)+g(x)的单调区间;
(2)若关于x的方程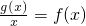 -2e(e为自然对数的底数)仅有有两个不等的实根,求a的取值范围.
-2e(e为自然对数的底数)仅有有两个不等的实根,求a的取值范围.
解:(1)函数F(x)的定义域为(0,+∞),F′(x)=1- +
+ =
= …(1分)
…(1分)
设h(x)=x2+x-a,方程x2+x-a=0的判别式△=1+4a,
①当△≤0时,即a≤- ,F'(x)>0,F(x)的单调增区间为(0,+∞),无单调减区间 …(3分)
,F'(x)>0,F(x)的单调增区间为(0,+∞),无单调减区间 …(3分)
②当△>0时,方程x2+x-a=0的两根为x1=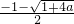 ,x2=
,x2= ,
,
(i)当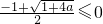 ,即-
,即- <a≤0时,F'(x)>0,
<a≤0时,F'(x)>0,
F(x)的单调增区间为(0,+∞),无单调减区间
(ii)当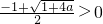 ,即a>0时,当x∈(0,
,即a>0时,当x∈(0, )时,F'(x)<0,
)时,F'(x)<0,
当x∈( ,+∞)时,F'(x)>0,
,+∞)时,F'(x)>0,
可得,当a>0时,F(x)的单调增区间为(0, ,单调减区间 (
,单调减区间 ( ,+∞).
,+∞).
(2)方程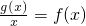 -2e=f(x)?
-2e=f(x)?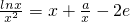 ?lnx=x2-a?
?lnx=x2-a?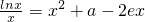 …(7分)
…(7分)
令G(x)= ,则G(x)的定义域为(0,+∞),
,则G(x)的定义域为(0,+∞),
G′(x)= >0,得0<x<e,∴G′(x)<0得x>e,
>0,得0<x<e,∴G′(x)<0得x>e,
所以G(x)在(0,e)上单调递增,在( e,+∞)上单调递减 …(10分)
G(x)min=G( e)= ,函数G(x)的大致图象如图所示.
,函数G(x)的大致图象如图所示.
令H(x)=x2-2ex+a,则H(x)在x=e时取得最小值H(e)=a-e 2,
关于x的方程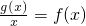 -2e(e为自然对数的底数)仅有有两个不等的实根,
-2e(e为自然对数的底数)仅有有两个不等的实根,
必有a-e2< ,∴a<e2+
,∴a<e2+
所以a的取值范围是a<e2+ …(12分)
…(12分)
分析:(1)求导,令导数大于零,对a分情况讨论,根据一元二次不等式的解的情况,即可求得结论;
(2)关于x的方程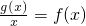 -2e恰有两个不等的实根,等价于
-2e恰有两个不等的实根,等价于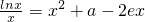 恰有两个不等的实根,令G(x)=
恰有两个不等的实根,令G(x)= ,利用导数工具,将问题转化为求函数的最值问题,即可求得结论.
,利用导数工具,将问题转化为求函数的最值问题,即可求得结论.
点评:掌握导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.考查了计算能力和分析解决问题的能力,体现了分类讨论和转化的数学思想.
 +
+ =
= …(1分)
…(1分)设h(x)=x2+x-a,方程x2+x-a=0的判别式△=1+4a,
①当△≤0时,即a≤-
 ,F'(x)>0,F(x)的单调增区间为(0,+∞),无单调减区间 …(3分)
,F'(x)>0,F(x)的单调增区间为(0,+∞),无单调减区间 …(3分)②当△>0时,方程x2+x-a=0的两根为x1=
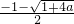 ,x2=
,x2= ,
,(i)当
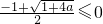 ,即-
,即- <a≤0时,F'(x)>0,
<a≤0时,F'(x)>0,F(x)的单调增区间为(0,+∞),无单调减区间
(ii)当
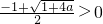 ,即a>0时,当x∈(0,
,即a>0时,当x∈(0, )时,F'(x)<0,
)时,F'(x)<0,当x∈(
 ,+∞)时,F'(x)>0,
,+∞)时,F'(x)>0,可得,当a>0时,F(x)的单调增区间为(0,
 ,单调减区间 (
,单调减区间 ( ,+∞).
,+∞).(2)方程
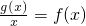 -2e=f(x)?
-2e=f(x)?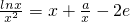 ?lnx=x2-a?
?lnx=x2-a?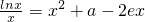 …(7分)
…(7分)令G(x)=
 ,则G(x)的定义域为(0,+∞),
,则G(x)的定义域为(0,+∞),G′(x)=
 >0,得0<x<e,∴G′(x)<0得x>e,
>0,得0<x<e,∴G′(x)<0得x>e,所以G(x)在(0,e)上单调递增,在( e,+∞)上单调递减 …(10分)
G(x)min=G( e)=
 ,函数G(x)的大致图象如图所示.
,函数G(x)的大致图象如图所示.
令H(x)=x2-2ex+a,则H(x)在x=e时取得最小值H(e)=a-e 2,
关于x的方程
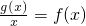 -2e(e为自然对数的底数)仅有有两个不等的实根,
-2e(e为自然对数的底数)仅有有两个不等的实根,必有a-e2<
 ,∴a<e2+
,∴a<e2+
所以a的取值范围是a<e2+
 …(12分)
…(12分)分析:(1)求导,令导数大于零,对a分情况讨论,根据一元二次不等式的解的情况,即可求得结论;
(2)关于x的方程
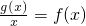 -2e恰有两个不等的实根,等价于
-2e恰有两个不等的实根,等价于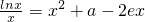 恰有两个不等的实根,令G(x)=
恰有两个不等的实根,令G(x)= ,利用导数工具,将问题转化为求函数的最值问题,即可求得结论.
,利用导数工具,将问题转化为求函数的最值问题,即可求得结论.点评:掌握导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.考查了计算能力和分析解决问题的能力,体现了分类讨论和转化的数学思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.