题目内容
若关于x的方程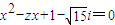 (其中z∈C)有实数根,在使得复数z的模取到最小时,该方程的解为 .
(其中z∈C)有实数根,在使得复数z的模取到最小时,该方程的解为 .
【答案】分析:当x为实数时,根据z的模的解析式,利用基本不等式求出z的模时,实数x=±2,求出对应的z值,从而得到对应的方程,解方程求得该方程的解.
解答:解:当x为实数时,由方程 (其中z∈C)可得
(其中z∈C)可得
z=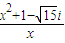 =x+
=x+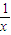 -
-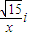 .
.
它的模为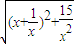 =
=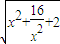 ≥2
≥2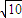 ,
,
当且仅当x2=4,即 x=±2时,取等号.
故满足条件的复数z=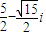 ,或 z=
,或 z=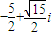 .
.
当z=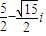 时,方程即
时,方程即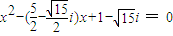 ,
,
此时,方程的一个根为x=2,另一个根为 x=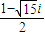 .
.
当 z=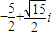 时,方程即
时,方程即 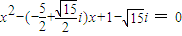 .
.
此时,方程的一个根为 x=-2,另一个根为 x=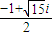 .
.
综上,该方程的解为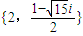 ,或
,或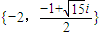 .
.
故答案为: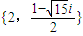 ,或
,或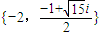 .
.
点评:本题考查虚数系数的一元二次方程的解法,复数模的定义和求法,基本不等式的应用,属于中档题.
解答:解:当x为实数时,由方程
 (其中z∈C)可得
(其中z∈C)可得z=
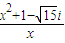 =x+
=x+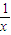 -
-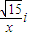 .
.它的模为
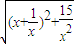 =
=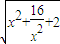 ≥2
≥2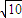 ,
,当且仅当x2=4,即 x=±2时,取等号.
故满足条件的复数z=
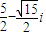 ,或 z=
,或 z=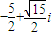 .
.当z=
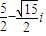 时,方程即
时,方程即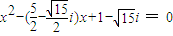 ,
,此时,方程的一个根为x=2,另一个根为 x=
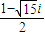 .
.当 z=
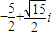 时,方程即
时,方程即 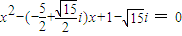 .
.此时,方程的一个根为 x=-2,另一个根为 x=
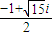 .
.综上,该方程的解为
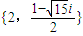 ,或
,或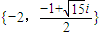 .
.故答案为:
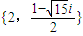 ,或
,或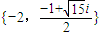 .
.点评:本题考查虚数系数的一元二次方程的解法,复数模的定义和求法,基本不等式的应用,属于中档题.

练习册系列答案
相关题目