题目内容
给出以下五个结论:(1)函数f(x)=
| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)若关于x的方程x-
| 1 |
| x |
(3)已知点P(a,b)与点Q(1,0)在直线2x-3y+1=0两侧,当a>0且a≠1,b>0时,
| b |
| a-1 |
| 1 |
| 3 |
| 2 |
| 3 |
(4)若将函数f(x)=sin(2x-
| π |
| 3 |
| 5π |
| 12 |
(5)已知m,n是两条不重合的直线,α,β是两个不重合的平面,若m⊥α,n∥β且m⊥n,则α⊥β;其中正确的结论是:
分析:根据反比例函数的性质及函数图象的平移变换法则,可以判断(1)的真假;根据方程根与函数零点的关系,利用图象法,易判断(2)的真假;根据平面点与直线的位置关系,可以求出a,b满足的不等式,进而得到点P(a,b)所对应的平面区域,分析
的几何意义,求出
的取值范围可判断(3)的真假;根据正弦型函数的对称性,及函数图象的平移变换,可判断(4)的真假;根据空间面面垂直的判定方法,即可判断(5)的真假.进而得到答案.
| b |
| a-1 |
| b |
| a-1 |
解答:解:函数f(x)=
的对称中心是(-
,
),故(1)错误;
若关于x的方程x-
+k=0在x∈(0,1)没有实数根,则k的取值范围是k≤0,故(2)错误;
点P(a,b)与点Q(1,0)在直线2x-3y+1=0两侧,则2a-3b+1<0,当a>0且a≠1,b>0时,
的取值范围为(-∞,-
)∪(
,+∞),故(3)正确;
若将函数f(x)=sin(2x-
)的图象向右平移?(?>0)个单位后变为偶函数,则φ=kπ+
,k∈N,当k=0时,?的最小值是
,故(4)正确;
若m⊥α,m⊥n,则n∥α,或n?α,又由n∥β,此时α与β可能平行也可能相交,故(5)错误
故答案为:(3)、(4)
| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
若关于x的方程x-
| 1 |
| x |
点P(a,b)与点Q(1,0)在直线2x-3y+1=0两侧,则2a-3b+1<0,当a>0且a≠1,b>0时,
| b |
| a-1 |
| 1 |
| 3 |
| 2 |
| 3 |
若将函数f(x)=sin(2x-
| π |
| 3 |
| 5π |
| 12 |
| 5π |
| 12 |
若m⊥α,m⊥n,则n∥α,或n?α,又由n∥β,此时α与β可能平行也可能相交,故(5)错误
故答案为:(3)、(4)
点评:本题考查的知识点是函数图象的平移变换,函数的对称性质,简单线性规划的应用,空间直线与平面位置关系的判定,方程根与函数零点的关系,其中熟练掌握相应基础知识点的熟练应用是解答本题的关键.

练习册系列答案
相关题目
 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, 给出以下命题:
给出以下命题: 时,
时, ;
;  的方程
的方程 有解,则实数
有解,则实数 的取值范围是
的取值范围是 ;
; 恒成立.其中,正确结论的代号是
.
恒成立.其中,正确结论的代号是
. 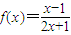 的对称中心是
的对称中心是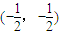 ;
;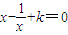 在x∈(0,1)没有实数根,则k的取值范围是k≥2;
在x∈(0,1)没有实数根,则k的取值范围是k≥2;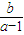 的取值范围为
的取值范围为 ;
;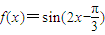 的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是
的图象向右平移ϕ(ϕ>0)个单位后变为偶函数,则ϕ的最小值是 ;
;