题目内容
已知锐角α、β满足sinα=
,sin(α-β)=-
,则β等于( )
| ||
| 5 |
| ||
| 10 |
分析:根据同角三角函数的基本关系求出cosα 和cos(α-β) 的值,再利用两角和差的余弦公式求出cosβ=cos[α-(α-β)]的值.
解答:解:∵锐角α、β满足sinα=
,sin(α-β)=-
,
则 cosα=
,cos(α-β)=
.
∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinα sin(α-β)
=
•
+
•( -
)=
,β=
,
故选B.
| ||
| 5 |
| ||
| 10 |
则 cosα=
2
| ||
| 5 |
3
| ||
| 10 |
∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinα sin(α-β)
=
2
| ||
| 5 |
3
| ||
| 10 |
| ||
| 5 |
| ||
| 10 |
| ||
| 2 |
| π |
| 4 |
故选B.
点评:本题主要考查同角三角函数的基本关系,两角和差的余弦公式的应用,属于基础题.

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: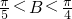 时,求△ABC的三边长及角B(用反三角函数值表示);
时,求△ABC的三边长及角B(用反三角函数值表示);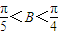 时,求△ABC的三边长及角B(用反三角函数值表示);
时,求△ABC的三边长及角B(用反三角函数值表示);