题目内容
 如右图,在平行四边形OABC中,点C(1,3),A(3,0).
如右图,在平行四边形OABC中,点C(1,3),A(3,0).(Ⅰ)求AB所在直线方程;
(Ⅱ)过点C作CD⊥AB于点D,求CD所在直线的方程.
分析:(1)求出AB 所在直线的向量,然后求出AB所在的直线方程;
(2)根据平行四边形的两条对边平行得到AB平行于OC,又CD垂直与AB,所以CD垂直与OC,由(1)求出的直线OC的斜率,根据两直线垂直时斜率乘积为-1,求出CD所在直线的斜率,然后根据求出的斜率和点C的坐标写出直线CD的方程即可.
(2)根据平行四边形的两条对边平行得到AB平行于OC,又CD垂直与AB,所以CD垂直与OC,由(1)求出的直线OC的斜率,根据两直线垂直时斜率乘积为-1,求出CD所在直线的斜率,然后根据求出的斜率和点C的坐标写出直线CD的方程即可.
解答:解:(1)∵AB∥OC,∴AD所在直线的斜率为:KAB=KOC=
=3.
∴AB所在直线方程是y-0=3(x-3),即3x-y-9=0.
(2)在平行四边形OABC中,AB∥OC,
∵CD⊥AB,
∴CD⊥OC.∴CD所在直线的斜率为kCD=-
.
∴CD所在直线方程为y-3=-
(x-1),即x+3y-10=0.
| 3-0 |
| 1-0 |
∴AB所在直线方程是y-0=3(x-3),即3x-y-9=0.
(2)在平行四边形OABC中,AB∥OC,
∵CD⊥AB,
∴CD⊥OC.∴CD所在直线的斜率为kCD=-
| 1 |
| 3 |
∴CD所在直线方程为y-3=-
| 1 |
| 3 |
点评:此题考查学生会根据两点的坐标求出过两点直线方程的斜率,掌握两直线平行时斜率所满足的条件,会根据一点和斜率写出直线的点斜式方程,是一道综合题.

练习册系列答案
相关题目
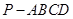 中,底面
中,底面 为平行四边形,
为平行四边形,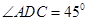 ,
,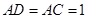 ,
, 为
为 中点,
中点, 平面
平面 ,
,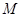 为
为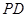 中点.
中点. //平面
//平面 ;
;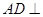 平面
平面 ;
;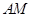 与平面
与平面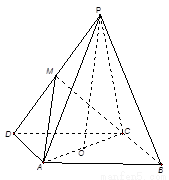
 中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )
中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( ) B.
B.
 D.
D.
 中,O是对角线AC,BD的交点,
中,O是对角线AC,BD的交点, B.
B.
 D.
D.
