题目内容
已知二次函数![]() 满足条件 :①对任意x∈R,均有
满足条件 :①对任意x∈R,均有![]() ②函数
②函数![]() 的图像与y=x相切.
的图像与y=x相切.
(1)求![]() 的解析式;
的解析式;
(2) 若函数![]() ,是否存在常数t (t≥0),当x∈[t,10]时,
,是否存在常数t (t≥0),当x∈[t,10]时,![]() 的值域为区间D,且D的长度为12-t,若存在,请求出t值,若不存在,请说明理由(注:
的值域为区间D,且D的长度为12-t,若存在,请求出t值,若不存在,请说明理由(注: ![]() 的区间长度为
的区间长度为![]() ).
).
解:(1)由①,a(x-4)^2+b(x-4)=a(2-x)^2+b(2-x),∴(2x-6)(-2a+b)=0,b=2a 2分
由②,ax^2+(2a-1)x=0的两根相等,∴a=1/2,b=1. f(x)=(1/2)x^2+x. 4分
所以g(x)=x2-16x+q+3.
(2)∵0≤t<10,f(x)在区间[0,8]上是减函数,在区间[8,10]上是增函数,且其图象的对称轴是x=8.
①当0≤t≤6时,在区间[t,10]上,f(t)最大,f(8)最小,
∴f(t)-f(8)=12-t,即t2-15t+52=0,
解得t=![]() ,∴t=
,∴t=![]() ;
;
②当6<t≤8时,在区间[t,10]上,f(10)最大,f(8)最小,
∴f(10)-f(8)=12-t,解得t=8;
③当8<t<10时,在区间[t,10]上,f(10)最大,f(t)最小,
∴f(10)-f(t)=12-t,即t2-17t+72=0,
解得t=8(舍去)或t=9.
综上可知,存在常数t为![]() ,8,9满足题意.
,8,9满足题意.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 满足条件
满足条件 ,及
,及 .
. 上的最大和最小值.
上的最大和最小值.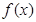 满足条件
满足条件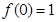 ,及
,及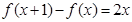 .
.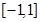 上的最值.
上的最值.