题目内容
如果曲线x2+4xy+3y2=1在矩阵
|
分析:通过对曲线进行化简变形,得到(x+y,y)在矩阵
的作用变为(x,y),建立等式即可求出a和b的值,即可求出所求.
|
解答:解:∵x2+4xy+3y2=1
∴(x+2y)2-y2=1在矩阵
的作用下变换得到曲线x2-y2=1,
则(x+2y,y)在矩阵
的作用变为(x,y)
即
=
=
∴2+a=0,b=0解得a=-2,b=0
∴a+b=-2
∴(x+2y)2-y2=1在矩阵
|
则(x+2y,y)在矩阵
|
即
|
|
|
|
∴2+a=0,b=0解得a=-2,b=0
∴a+b=-2
点评:本题主要考查了几种特殊的矩阵变换,以及待定系数法的求解等有关知识,属于基础题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
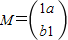 的作用下变换为曲线x2-2y2=1,求M的逆矩阵M-1= .
的作用下变换为曲线x2-2y2=1,求M的逆矩阵M-1= .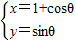 (θ为参数),在曲线C1求一点,使它到直线C2:
(θ为参数),在曲线C1求一点,使它到直线C2: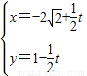 (t为参数)的距离最小,最小距离 .
(t为参数)的距离最小,最小距离 . .试求a的取值范围 .
.试求a的取值范围 . 的作用下变换得到曲线x2-y2=1,求a+b的值.
的作用下变换得到曲线x2-y2=1,求a+b的值. 的作用下变换得到曲线x2-y2=1,求a+b的值.
的作用下变换得到曲线x2-y2=1,求a+b的值.