题目内容
本题有(1)、(2)、(3)三个选考题,请考生任选2题作答,如果多做,则按所做的前两题计分.(1)选修4-2:矩阵与变换曲线x2+4xy+2y2=1在二阶矩阵
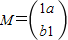 的作用下变换为曲线x2-2y2=1,求M的逆矩阵M-1= .
的作用下变换为曲线x2-2y2=1,求M的逆矩阵M-1= .(2)选修4-4:坐标系与参数方程在曲线C1:
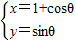 (θ为参数),在曲线C1求一点,使它到直线C2:
(θ为参数),在曲线C1求一点,使它到直线C2: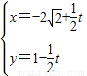 (t为参数)的距离最小,最小距离 .
(t为参数)的距离最小,最小距离 .(3)选修4-5:不等式选讲设函数f(x)=
 .试求a的取值范围 .
.试求a的取值范围 .
【答案】分析:(1)由detM=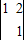 =1,能求出M-1.
=1,能求出M-1.
(2)将直线的参数方程化为普通方程,曲线C1任意点P的坐标为(1+cosθ,sinθ),利用点到直线的距离公式P到直线的距离d,分子合并后利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,与分母约分化简后,根据正弦函数的值域可得正弦函数的最小值,进而得到距离d的最小值,并求出此时θ的度数,即可确定出所求点P的坐标.
(3)由f(x)=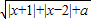 ,知|x+1|+|x-2|+a≥0,由此能求出a的取值范围.
,知|x+1|+|x-2|+a≥0,由此能求出a的取值范围.
解答:解:(1)∵detM=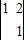 =1,
=1,
∴M-1=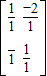 =
=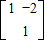 .
.
故答案为: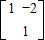 .
.
(2)将直线C2化为普通方程得:x+y-1+2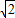 =0,
=0,
设所求的点为P(1+cosθ,sinθ),
则P到直线C2的距离d=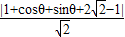
=|sin(θ+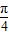 )+2|,
)+2|,
当θ+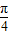 =
=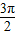 ,即θ=
,即θ=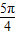 时,sin(θ+
时,sin(θ+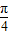 )=-1,d取得最小值1,
)=-1,d取得最小值1,
此时点P的坐标为(1-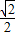 ,-
,- ).
).
故答案为:1.
(3)∵f(x)=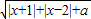 ,
,
∴|x+1|+|x-2|+a≥0,
∵|x+1|+|x-2|≥3,
∴a≥-3.
故答案为:{a|a≥-3}.
点评:第(1)题考查矩阵与变换的应用,第(2)题考查坐标系与参数方程的应用,第(3)题考查不等式的应用,解题时要认真审题,注意等价转化思想的合理运用.
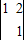 =1,能求出M-1.
=1,能求出M-1.(2)将直线的参数方程化为普通方程,曲线C1任意点P的坐标为(1+cosθ,sinθ),利用点到直线的距离公式P到直线的距离d,分子合并后利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,与分母约分化简后,根据正弦函数的值域可得正弦函数的最小值,进而得到距离d的最小值,并求出此时θ的度数,即可确定出所求点P的坐标.
(3)由f(x)=
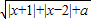 ,知|x+1|+|x-2|+a≥0,由此能求出a的取值范围.
,知|x+1|+|x-2|+a≥0,由此能求出a的取值范围.解答:解:(1)∵detM=
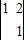 =1,
=1,∴M-1=
 =
=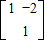 .
.故答案为:
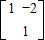 .
.(2)将直线C2化为普通方程得:x+y-1+2
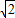 =0,
=0,设所求的点为P(1+cosθ,sinθ),
则P到直线C2的距离d=
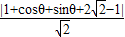
=|sin(θ+
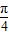 )+2|,
)+2|,当θ+
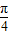 =
=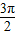 ,即θ=
,即θ=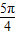 时,sin(θ+
时,sin(θ+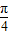 )=-1,d取得最小值1,
)=-1,d取得最小值1,此时点P的坐标为(1-
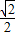 ,-
,- ).
).故答案为:1.
(3)∵f(x)=
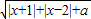 ,
,∴|x+1|+|x-2|+a≥0,
∵|x+1|+|x-2|≥3,
∴a≥-3.
故答案为:{a|a≥-3}.
点评:第(1)题考查矩阵与变换的应用,第(2)题考查坐标系与参数方程的应用,第(3)题考查不等式的应用,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目