Question

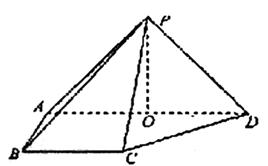
（08年福建卷文）（本小题满分14分）

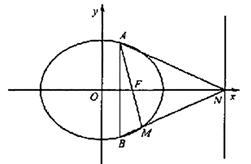
如图，椭圆的一个焦点是，且过点。

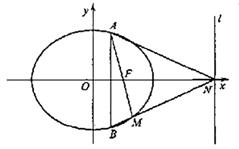
（Ⅰ）求椭圆C的方程；

（Ⅱ）若AB为垂直于x轴的动弦，直线与x轴交于点N，直线AF与BN交于点M。

    （）求证：点M恒在椭圆C上；

（）求面积的最大值。

Answer 1

解析：本小题主要考查直线与椭圆的位置关系、轨迹方程、不等式等基本知识，考查运算能力和综合解题能力。

解法一：

（Ⅰ）由题设，从而，

所以椭圆C的方程为。

（Ⅱ）（）由题意得。

设则，。 ……………………………… ①

与的方程分别为：

。

设，则有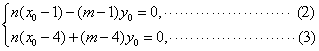

由②，③得。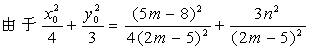

。

所以点M恒在椭圆C上。

（）设AM的方程为，代入得。

设，则有：。

。

令，则

，

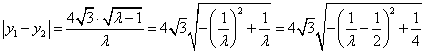因为，

有最大值3，此时AM过点F。

△AMN的面积有最大值。

解法二：

（Ⅰ）同解法一：

（Ⅱ）（）由题意得。

设则，。 ……………………………… ①

与的方程分别为： …………………………… ②

…………………………… ③

由②，③得：当时，。………………………… ④

由④代入①，得。

当时，由②，③得：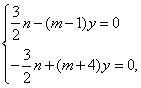

解得    与矛盾。

所以点M的轨迹方程为即点M恒在椭圆C上。

（Ⅱ）同解法一。