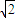题目内容
已知x>1,y>2,且xy=32,则(log2x)•(log2
)的最大值为( )
| y |
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
分析:先根据基本不等式将(log2x)•(log2
)放缩,然后根据对数运算得到答案.
| y |
| 2 |
解答:解:∵(log2x)•(log2
)≤(
)2=(
)2=4(当且仅当log2x=log2
,即x=4,y=8时等号取到)
∴(log2x)•(log2
)的最大值为4
故选D.
| y |
| 2 |
log2x+log2
| ||
| 2 |
log2(x•
| ||
| 2 |
| y |
| 2 |
∴(log2x)•(log2
| y |
| 2 |
故选D.
点评:本题主要考查对数函数的运算性质和基本不等式的运用.属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的最大值为
的最大值为
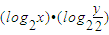 的最大值为( )
的最大值为( )