题目内容
如图,AB为抛物线y=x2上的动弦，且|AB|=a（a为常数，且a≥1），求弦AB的中点M离x轴的最近距离.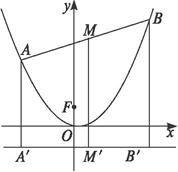
思路解析：利用定义把|AB|转化为到x轴的距离问题，易求.
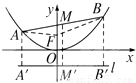
解：设A、M、B点的纵坐标分别为y1、y2、y3，A、M、B三点在抛物线准线上的射影分别为A′、M′、B′.
由抛物线的定义，|AF|=|AA′|=y1+
,|BF|=|BB′|=y3+
.
∴y1=|AF|-
,y3=|BF|-
.
又M是线段AB的中点，∴y2=
(y1+y3)=
(|AF|+|BF|-
)≥
×(|AB|-
)=
(2a-1).
等号在AB过焦点F时成立，即当定长为a的弦AB过焦点F时，M点与x轴的距离最近，最近距离为
（2a-1）.
练习册系列答案
相关题目
如图，AB为抛物线y=x2上的动弦，且|AB|=a（a为常数且a≥1），求弦AB的中点M与x轴的最短距离．
（2010•潍坊三模）如图，过抛物线C1：y=x2-1上一点P（不与顶点重合）的切 线l与曲线C2：
x3+
(a-1)x2+bx(a、b为常数)在x=1和x=4处取得极值.