题目内容
如图,AB为抛物线y=x2上的动弦,且|AB|=a(a为常数且a≥1),求弦AB的中点M与x轴的最短距离.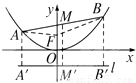
【答案】分析:设A、M、B三点的纵坐标分别为y1、y2、y3,如图,A、M、B三点在抛物线准线上的射影分别为A′、M′、B′.
F为抛物线的焦点.连接AA′,MM′,BB′,AF,BF.由抛物线的定义可知:|AF|=|AA′|=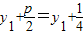 ,
,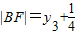 .又M是线段AB的中点,利用梯形的中位线定理可得
.又M是线段AB的中点,利用梯形的中位线定理可得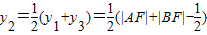
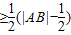 ,解出即可.
,解出即可.
解答:解:设A、M、B三点的纵坐标分别为y1、y2、y3,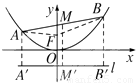 如图,
如图,
A、M、B三点在抛物线准线上的射影分别为A′、M′、B′.
F为抛物线的焦点.连接AA′,MM′,BB′,AF,BF.
由抛物线的定义可知:|AF|=|AA′|=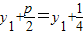 ,
,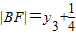 .
.
∴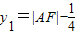 ,
,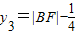 .
.
又M是线段AB的中点,∴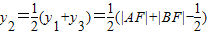
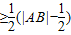 =
=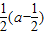 .
.
当且仅当AB过焦点F时,等号成立.
即当定长为a的弦AB过焦点F时,弦AB的中点M与x轴的距离最小,最小值为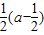 .
.
点评:熟练掌握抛物线的定义、梯形的中位线定理及其三角形的三边的大小关系和三点共线是解题的关键.
F为抛物线的焦点.连接AA′,MM′,BB′,AF,BF.由抛物线的定义可知:|AF|=|AA′|=
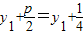 ,
,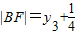 .又M是线段AB的中点,利用梯形的中位线定理可得
.又M是线段AB的中点,利用梯形的中位线定理可得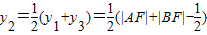
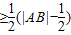 ,解出即可.
,解出即可.解答:解:设A、M、B三点的纵坐标分别为y1、y2、y3,
 如图,
如图,A、M、B三点在抛物线准线上的射影分别为A′、M′、B′.
F为抛物线的焦点.连接AA′,MM′,BB′,AF,BF.
由抛物线的定义可知:|AF|=|AA′|=
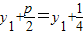 ,
,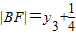 .
.∴
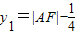 ,
,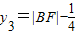 .
.又M是线段AB的中点,∴
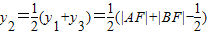
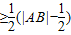 =
=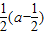 .
.当且仅当AB过焦点F时,等号成立.
即当定长为a的弦AB过焦点F时,弦AB的中点M与x轴的距离最小,最小值为
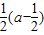 .
.点评:熟练掌握抛物线的定义、梯形的中位线定理及其三角形的三边的大小关系和三点共线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB为抛物线y=x2上的动弦,且|AB|=a(a为常数且a≥1),求弦AB的中点M与x轴的最短距离.
如图,AB为抛物线y=x2上的动弦,且|AB|=a(a为常数且a≥1),求弦AB的中点M与x轴的最短距离.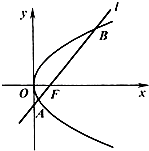 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.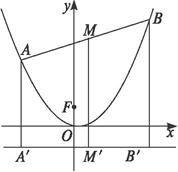
 (1)求使△PAB的面积最大的P点的坐标(a,b);
(1)求使△PAB的面积最大的P点的坐标(a,b);