Question

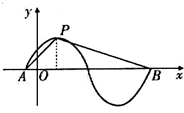若函数y=sin（πx+φ）（φ＞0）的两部分图象如图，设p是图象的最高点，A、B是图象与x轴的交点，设∠PAB=θ，则tanθ的值是（　　）

Answer 1

分析：由解析式求出函数的周期与最值，做出辅助线过p作PD⊥x轴于D，根据周期的大小看出直角三角形APD中直角边的长度，解出∠PAB的正切．

解答：解：∵函数y=sin（πx+φ）
∴T=

2π

π

=2，最大值为1，
过p作PD⊥x轴于D，则AD是四分之一个周期，有AD=

1

2

，在直角三角形PAD中有tan∠PAB=

PD

AD

=

1

1 2

=2．
故选C．

点评：本题考查了正弦函数的周期，把要求的角放到直角三角形中，利用三角函数的定义得到结果．