题目内容
已知中心在原点、焦点在x轴上的椭圆的离心率是
，椭圆上任意一点到两个焦点距离之和为4．（1）求椭圆标准方程；
（2）设椭圆长轴的左端点为A，P是椭圆上且位于第一象限的任意一点，AB∥OP，点B在椭圆上，R为直线AB与y轴的交点，证明：
．
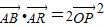【答案】分析：（1）由题意设出椭圆的标准方程，根据椭圆的离心率结合长轴长及c2=a2-b2即可求得答案；
（2）由椭圆方程求出A的坐标，设出P、B、R的坐标，由P和点B都在椭圆上得两点的坐标适合椭圆方程，再由AB∥OP得其斜率相等，列式得到P、B两点坐标的关系式，写出直线AB的方程，把R的坐标代入AB的方程得到B和R的坐标的关系式，然后运用坐标的关系分别表示出等式
的左右两边，从而问题得到证明．
解答：（1）解：根据题设，可设椭圆标准方程为：
则离心率
，由椭圆定义，得2a=4
解得a=2，
所以椭圆标准方程为：
（2）证明：由题意得A（-2，0），设P（x1，y1），B（x2，y2），R（0，y3），其中x1＞0，y1＞0，
点P和点B都在椭圆上，则有
①
②
由AB∥OP，有
，
即
③
由x1＞0，y1＞0可知x2≠-2．
AB直线方程为：y-0=kAB[x-（-2）]，即
．
把R（0，y3）代入，得
所以有
，
，
，
可得：
④
⑤
由①，②，③得：
⑥
由①，⑤得：
⑦
由②，④得：
⑧
由⑦，⑥得：
⑨
由⑧，⑨可证得：
．
点评：本题主要考查了椭圆的标准方程，考查了直线与圆锥曲线的位置关系的应用，训练了代值思想方法，解答此题的关键是在设出点的坐标后能找到各坐标之间的关系，要求考生具备较强的运算推理的能力，是难题．
（2）由椭圆方程求出A的坐标，设出P、B、R的坐标，由P和点B都在椭圆上得两点的坐标适合椭圆方程，再由AB∥OP得其斜率相等，列式得到P、B两点坐标的关系式，写出直线AB的方程，把R的坐标代入AB的方程得到B和R的坐标的关系式，然后运用坐标的关系分别表示出等式
的左右两边，从而问题得到证明．解答：（1）解：根据题设，可设椭圆标准方程为：
则离心率
，由椭圆定义，得2a=4解得a=2，
所以椭圆标准方程为：
（2）证明：由题意得A（-2，0），设P（x1，y1），B（x2，y2），R（0，y3），其中x1＞0，y1＞0，
点P和点B都在椭圆上，则有
①②由AB∥OP，有
，即
③由x1＞0，y1＞0可知x2≠-2．
AB直线方程为：y-0=kAB[x-（-2）]，即
．把R（0，y3）代入，得
所以有
，，，可得：
④⑤由①，②，③得：
⑥由①，⑤得：
⑦由②，④得：
⑧由⑦，⑥得：
⑨由⑧，⑨可证得：
．点评：本题主要考查了椭圆的标准方程，考查了直线与圆锥曲线的位置关系的应用，训练了代值思想方法，解答此题的关键是在设出点的坐标后能找到各坐标之间的关系，要求考生具备较强的运算推理的能力，是难题．
练习册系列答案
相关题目