题目内容
15.中心角为135°的扇形,其面积为S1,其围成的圆锥的全面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{11}{8}$ | B. | $\frac{13}{8}$ | C. | $\frac{8}{11}$ | D. | $\frac{8}{13}$ |
分析 设扇形半径为1,l为扇形弧长,也为圆锥底面周长,由扇形面积公式求得侧面积,再利用展开图的弧长为底面的周长,求得底面半径,进而求底面面积,从而求得表面积,最后两个结果取比即可.
解答 解:设扇形半径为1,则扇形弧长为1×$\frac{3π}{4}$=$\frac{3π}{4}$,
设围成圆锥的底面半径为r,则2πr=$\frac{3π}{4}$,r=$\frac{3}{8}$,
扇形的面积S1=$\frac{1}{2}$×1×$\frac{3π}{4}$=$\frac{3π}{8}$,圆锥的表面积S2=S1+πr2=$\frac{3π}{8}$+$\frac{9π}{64}$=$\frac{33π}{64}$,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{8}{11}$.
故选:C.
点评 本题主要考查圆锥的侧面积和表面积的求法,同时,还考查了平面与空间图形的转化能力,属基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
6.平面内有一长度为4的线段AB,动点P满足|PA|+|PB|=6,则点P的轨迹是( )
| A. | 直线 | B. | 射线 | C. | 椭圆 | D. | 双曲线 |
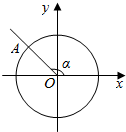 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为$\frac{2}{3}$,则cosα=-$\frac{\sqrt{5}}{3}$.
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为$\frac{2}{3}$,则cosα=-$\frac{\sqrt{5}}{3}$.