题目内容
已知数列{an}的各项均为正数,前n项和为Sn,且满足2Sn=a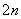 +n-4(n∈N*).
+n-4(n∈N*).
(1)求证:数列{an}为等差数列;
(2)求数列{an}的通项公式.
解:(1)证明:当n=1时,有2a1=a +1-4,
+1-4,
即a -2a1-3=0,
-2a1-3=0,
解得a1=3(a1=-1舍去).
当n≥2时,有2Sn-1=a +n-5,
+n-5,
又2Sn=a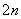 +n-4,
+n-4,
两式相减得2an=a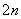 -a
-a +1,
+1,
即a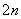 -2an+1=a
-2an+1=a ,也即(an-1)2=a
,也即(an-1)2=a ,
,
因此an-1=an-1或an-1=-an-1.
若an-1=-an-1,则an+an-1=1.
而a1=3,所以a2=-2,这与数列{an}的各项均为正数相矛盾,所以an-1=an-1,
即an-an-1=1,因此数列{an}为首项为3,公差为1的等差数列.
(2)由(1)知a1=3,d=1,
所以数列{an}的通项公式
an=3+(n-1)×1=n+2,即an=n+2.

练习册系列答案
相关题目
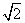 n mile.此船的航速是________n mile/h.
n mile.此船的航速是________n mile/h. 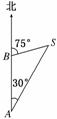
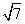 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过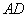 作圆柱的截面交下底面于
作圆柱的截面交下底面于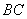 , 四边形ABCD是正方形.
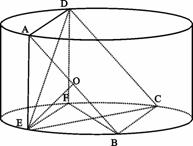
, 四边形ABCD是正方形. ;
;
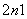 =anan+2”的( )
=anan+2”的( )
 在区间
在区间 内
内 个零点 C.有且仅有
个零点 C.有且仅有 个零点 D.有且仅有
个零点 D.有且仅有 个零点
个零点