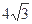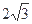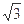题目内容
一个四面体的顶点在空间直角坐系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为( )
A. |
B. |
C. |
D. |
A
解析

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为 、
、 ,则
,则 :
: =( ).
=( ).
| A.1:1 | B.2:1 | C.3:2 | D.4:1 |
一个几何体的正视图、侧视图、和俯视图形状都相同,大小均相等,则这个几何体不可以是( )
| A.球 | B.三棱锥 | C.正方体 | D.圆柱 |
右图是棱长为2的正方体的表面展开图,则多面体 的体积为( )
的体积为( )
| A.2 | B. | C. | D. |
一个几何体的三视图如图所示,则此几何体的体积是( )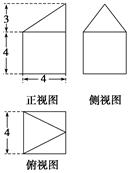
| A.112 | B.80 | C.72 | D.64 |
已知三棱锥的三视图如图所示,则它的外接球表面积为( )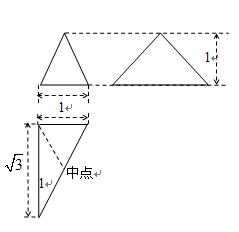
A. |
B.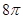 |
C.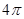 |
D.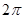 |
某几何体的三视图如图所示,它的体积为
A.12 |
B.45 |
C.57 |
D.81 |
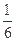 ,经过3个点的小圆的周长为
,经过3个点的小圆的周长为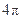 ,那么这个球的半径为( )
,那么这个球的半径为( )