题目内容
已知定点
，F是椭圆
的右焦点，M是椭圆上一点，满足|AM|+2|MF|的值最小，则点M的坐标和|AM|+2|MF|的最小值分别为（ ）A．
B．
C．
D．
【答案】分析：利用圆锥曲线的统一定义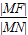
=e=
，结合题意化简得|AM|+2|MF|=|AM|+|MN|，根据平面几何性质得当A、M、N共线于垂直于右准线的一条直线上时，|AM|+2|MF|取得最小值，由此即可算出答案．
解答：解：∵椭圆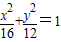
中，a=4，b=2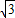
∴c=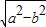
=2，离心率e=
=
，
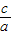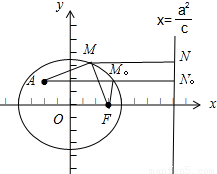
记点M（m，n）到右准线的距离为|MN|，
则根据圆锥曲线的统一定义，得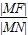
=e=
，
可得|MN|=2|MF|，从而得到|AM|+2|MF|=|AM|+|MN|，
由此可得：当A，M，N同时在垂直于右准线的一条直线上时，
|AM|+2|MF|取得最小值，此时M的纵坐标与A点相等，
即n=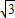
，代入到椭圆方程，解得m=±2，
而点M在第一象限，可得M（2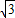
，
），
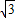由椭圆的准线方程为x=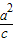
=8，可得|AM|+2|MF|的最小值为8-（-2）=10
故选：C
点评：本题给出定点A和焦点为F的椭圆上的动点M，求|AM|+2|MF|的最小值．着重考查了椭圆的标准方程与简单几何性质、圆锥曲线的统一定义等知识，属于中档题．
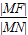=e=，结合题意化简得|AM|+2|MF|=|AM|+|MN|，根据平面几何性质得当A、M、N共线于垂直于右准线的一条直线上时，|AM|+2|MF|取得最小值，由此即可算出答案．解答：解：∵椭圆
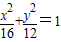中，a=4，b=2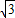∴c=
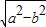=2，离心率e=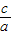=，记点M（m，n）到右准线的距离为|MN|，
则根据圆锥曲线的统一定义，得
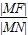=e=，可得|MN|=2|MF|，从而得到|AM|+2|MF|=|AM|+|MN|，
由此可得：当A，M，N同时在垂直于右准线的一条直线上时，
|AM|+2|MF|取得最小值，此时M的纵坐标与A点相等，
即n=
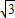，代入到椭圆方程，解得m=±2，而点M在第一象限，可得M（2
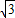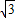，），由椭圆的准线方程为x=
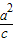=8，可得|AM|+2|MF|的最小值为8-（-2）=10故选：C
点评：本题给出定点A和焦点为F的椭圆上的动点M，求|AM|+2|MF|的最小值．着重考查了椭圆的标准方程与简单几何性质、圆锥曲线的统一定义等知识，属于中档题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
＋
＝1(a＞b＞c)与圆F：(x－c)2＋y2＝9的一个交点，且圆心F是椭圆的一个焦点，(1)求椭圆C的方程；(2)过F的直线交圆与P、Q两点，连AP、AQ分别交椭圆与M、N点，试问直线MN是否过定点？若过定点，则求出定点坐标；若不过定点，请说明理由．
是椭圆C：
与圆F：
的一个交点，且圆心F是椭圆的一个焦点，（1）求椭圆C的方程；（2）过F的直线交圆与P、Q两点，连AP、AQ分别交椭圆与M、N点，试问直线MN是否过定点？若过定点，则求出定点坐标；若不过定点，请说明理由．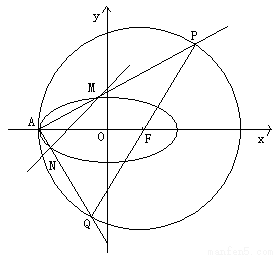
，F是椭圆
的右焦点，在椭圆上求一点M，使|AM|+2|MF|取得最小值．
，F是椭圆
的左焦点，点M在椭圆上，若使|PM|+2|MF|最小，则点M的坐标为 ．