题目内容
14.在△ABC中,a,b,c为角A,B,C的对边,若A=$\frac{π}{6}$,cosB=$\frac{3}{5}$,b=8,则a=( )| A. | $\frac{40}{3}$ | B. | 10 | C. | $\frac{20}{3}$ | D. | 5 |
分析 结合B的范围,由已知及同角三角函数关系式可求sinB,利用正弦定理即可求得a的值.
解答 解:∵cosB=$\frac{3}{5}$,0<B<π,
∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{4}{5}$,
∴由正弦定理可得:a=$\frac{bsinA}{sinB}$=$\frac{8×sin\frac{π}{6}}{\frac{4}{5}}$=5.
故选:D.
点评 本题主要考查了同角三角函数关系式,正弦定理的应用,属于基础题.

练习册系列答案
相关题目
3.如图,在复平面内,复数z1和z2对应的点分别是A和B,则$\frac{{z}_{1}}{{z}_{2}}$等于( )
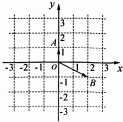

| A. | $\frac{1}{5}$+$\frac{2}{5}$i | B. | $\frac{2}{5}$+$\frac{1}{5}$i | C. | -$\frac{1}{5}$+$\frac{2}{5}$i | D. | -$\frac{2}{5}$+$\frac{1}{5}$i |