题目内容
已知sin(θ+π)<0,cos(θ-π)>0,则下列不等关系中必定成立的是( )
| A.sinθ<0,cosθ>0 | B.sinθ>0,cosθ<0 | C.sinθ>0,cosθ>0 | D.sinθ<0,cosθ<0 |
B
解析试题分析:解:因为sin(θ+π)<0,所以-sinθ<0,即sinθ>0;又因为cos(θ-π)>0,所以-cosθ>0,即cosθ<0.故选B
考点:诱导公式
点评:本题考查三角函数的诱导公式的运用,属于基础题。关键是能根据对与诱导公式的准确化简和表示。

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
函数 的图象上一点
的图象上一点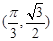 处的切线的斜率为
处的切线的斜率为
| A.1 | B.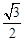 | C. | D.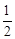 |
要得到函数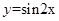 的图象,可以将
的图象,可以将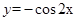 的图象( )
的图象( )
A.向左平移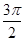 | B.向右平移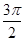 | C.向左平移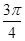 | D.向右平移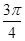 |
已知 ,则
,则 =( )
=( )
A. | B. | C. | D. |
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
函数 (其中A>0,
(其中A>0, )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,则只需将g(x)=sin2x的图象
的图象,则只需将g(x)=sin2x的图象
A.向右平移 个长度单位 个长度单位 |
B.向左平移 个长度单位 个长度单位 |
C.向右平移 个长度单位 个长度单位 |
D.向左平移 个长度单位 个长度单位 |
化简sin 2013o的结果是
| A.sin 33o | B.cos33o | C.-sin 33o | D.-cos33o |
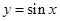 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的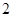 倍(纵坐标不变),所得图像的函数解析式是( )
倍(纵坐标不变),所得图像的函数解析式是( )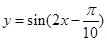
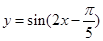
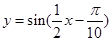
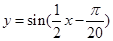
 ,那么三边长a、b、c之间满足的关系是( )
,那么三边长a、b、c之间满足的关系是( ) B.
B. C.
C. D.
D.