题目内容
在等比数列{an}中，a1=1，a10=3，若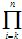
ai=ak•aK+1…an，则
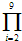ai=
ai=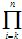ak•aK+1…an，则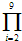ai=81
81
．分析：由题中已知的新定义表示出所求的式子，把项数之和为11的两项结合，利用等比数列的性质化简后，将a1及a10的值代入即可求出值．
解答：解：∵等比数列{an}中，a1=1，a10=3，
∴a2a9=a3a8=a4a7=a5a6=a1a10=3，
∴a2a3a4a5a6a7a8a9=(a2a9)(a3a8)(a4a7)(a5a6)=(a1a10)4=34=81，
则所求的式子等于81．
故答案为：81
∴a2a9=a3a8=a4a7=a5a6=a1a10=3，
∴a2a3a4a5a6a7a8a9=(a2a9)(a3a8)(a4a7)(a5a6)=(a1a10)4=34=81，
则所求的式子等于81．
故答案为：81
点评：此题考查了等比数列的性质，属于新定义的题型，熟练掌握等比数列的性质是解本题的关键．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
在等比数列{an}中，若a1=1，公比q=2，则a12+a22+…+an2=（ ）
| A、（2n-1）2 | ||
B、
| ||
| C、4n-1 | ||
D、
|