题目内容
(本题满分12分)如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=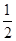 BD
BD
(1)求证:BF∥平面ACE;
(2)求二面角B-AF-C的大小;
(3)求点F到平面ACE的距离.
练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
题目内容
(本题满分12分)如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=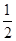 BD
BD
(1)求证:BF∥平面ACE;
(2)求二面角B-AF-C的大小;
(3)求点F到平面ACE的距离.
 优学名师名题系列答案
优学名师名题系列答案