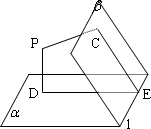
题目内容
 如图,在平面角为600的二面角
如图,在平面角为600的二面角![]() -l-
-l-![]() 内有一点P,P到
内有一点P,P到![]() 、
、![]() 分别为PC=2cm,PD=3cm,则垂足的连线CD等于多少?(2)P到棱l的距离为多少?
分别为PC=2cm,PD=3cm,则垂足的连线CD等于多少?(2)P到棱l的距离为多少?
解析:
对于本题若这么做:过C在平面![]() 内作棱l的垂线,垂足为E,连DE,则
内作棱l的垂线,垂足为E,连DE,则![]() CED即为二面角的平面角。这么作辅助线看似简单,实际上在证明
CED即为二面角的平面角。这么作辅助线看似简单,实际上在证明![]() CED为二面角的平面角时会有一个很麻烦的问题,需要证明P、D、E、C四点共面。这儿,可以通过作垂面的方法来作二面角的平面角。
CED为二面角的平面角时会有一个很麻烦的问题,需要证明P、D、E、C四点共面。这儿,可以通过作垂面的方法来作二面角的平面角。
解:∵PC、PD是两条相交直线,
∴PC、PD确定一个平面![]() ,设
,设![]() 交棱l于E,连CE、DE。
交棱l于E,连CE、DE。
∵PC⊥![]() , ∴PC⊥l,
, ∴PC⊥l,
又∵PD⊥![]() ,∴PD⊥l。
,∴PD⊥l。
∴l⊥平面![]() ,则l⊥CE、DE,故
,则l⊥CE、DE,故![]() CED即为二面角的平面角,即
CED即为二面角的平面角,即![]() CED=600。
CED=600。
∴![]() CPD=1200,△PCD中,PD=3,PC=2,由余弦定理得CD=
CPD=1200,△PCD中,PD=3,PC=2,由余弦定理得CD=![]() cm。由PD⊥DE,PC⊥CE可得P、D、E、C四点共圆,且PE为直径,由正弦定理得PE=2R=
cm。由PD⊥DE,PC⊥CE可得P、D、E、C四点共圆,且PE为直径,由正弦定理得PE=2R=![]() =
=![]() =
=![]() cm。
cm。
说明:三垂线定理及其逆定理是作二面角的平面角的最主要的方法,要引起重视。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

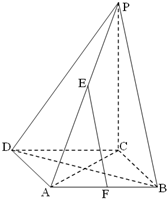 如图,在边长为a的菱形ABCD中,∠ABC=60°,PC⊥面ABCD,PC=2a,E、F分别是PA和AB的中点.
如图,在边长为a的菱形ABCD中,∠ABC=60°,PC⊥面ABCD,PC=2a,E、F分别是PA和AB的中点.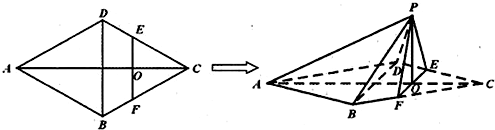
 (2012•许昌三模)如图,在四面体ABCD中,二面角A-CD-B的平面角为60°,AC⊥CD,BD⊥CD,且AC=CD=2BD,点E、F分别是AD、BC的中点.
(2012•许昌三模)如图,在四面体ABCD中,二面角A-CD-B的平面角为60°,AC⊥CD,BD⊥CD,且AC=CD=2BD,点E、F分别是AD、BC的中点.