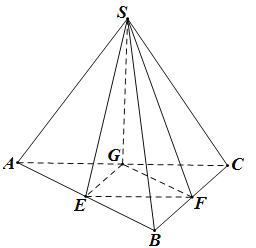
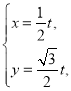��Ŀ����
����Ŀ����Ʒ�۸�����Ʒ�������Ǿ���ѧ�е�һ�ֻ�����ϵ��ij��װ��˾��������е�һ���װ�ƶ������ļ۸���Ҫ�˽��װ�ĵ���x����λ��Ԫ����������y����λ��������������z����λ��Ԫ����Ӱ�죬������10���µļ۸�![]() ����������
����������![]() ��
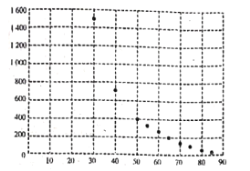
��![]() ���������˳����������õ���ͼ��ʾ��ɢ��ͼ��һЩͳ������ֵ.
���������˳����������õ���ͼ��ʾ��ɢ��ͼ��һЩͳ������ֵ.
x |
| y |
|
|
|
|
61 | 0.018 | 372 |
| 2670 | 26 | 0.0004 |
����![]() .
.
��1������ɢ��ͼ�жϣ�![]() ��
��![]() ��һ��������Ϊ������y���ڼ۸�x�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
��һ��������Ϊ������y���ڼ۸�x�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ�
��2�����ݣ�1�����жϽ�����������ݣ�����y����x�Ļع鷽�̣�
��3����֪������װ�ijɱ�Ϊÿ��10Ԫ�����ݣ�1���Ľ���ش��������⣻
��i��Ԥ���װ�۸�![]() ʱ������������Ԥ��ֵ�Ƕ��٣�
ʱ������������Ԥ��ֵ�Ƕ��٣�
��span>ii������װ�۸�xΪ��ֵʱ���������Ԥ��ֵ����ο�����![]() ��
��
��������һ�����ݣ���ع�ֱ�ߵ�б�ʺͽؾ����С���˹��Ʒֱ�Ϊ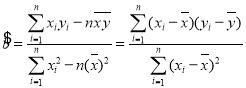 .
.
���𰸡���1��![]() ����2��
����2��![]() ����3����i��502����ii������װ�۸�
����3����i��502����ii������װ�۸�![]() ʱ���������Ԥ��ֵ���.
ʱ���������Ԥ��ֵ���.
��������
��1������ɢ��ͼ����Ϻ���ͼ���������жϣ�
��2�����ݲο����ݣ��Ƚ���y��w�����Իع鷽�̣��ٽ���ת��Ϊ![]() ��
��![]() ֮��ĺ������ɣ�
֮��ĺ������ɣ�
��3�����������ݣ�2��������ع鷽�̣����ɴ�ֵ��⣻
���������ݣ�2�������������ļ��㣬���þ�ֵ����ʽ�������.
��1����ɢ��ͼ�����жϣ�![]() ��Ϊ������
��Ϊ������![]() ���ڼ۸�
���ڼ۸�![]() �Ļع鷽������.
�Ļع鷽������.
��2����![]() �Ƚ���
�Ƚ���![]() ��
��![]() �����Իع鷽�̣�
�����Իع鷽�̣�
����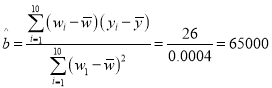
![]() ��
��
����![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() ��
��
���![]() ����
����![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]() .
.
��3���������ɣ�2����֪���۸�![]() ʱ��
ʱ��
�����ۼ�![]() ��Ԥ��ֵΪ
��Ԥ��ֵΪ![]() .
.
�������ɣ�2����֪�������Ԥ��ֵΪ![]() ��
��
���Ե�![]() ����
����![]() ʱ���������Ԥ��ֵ���
ʱ���������Ԥ��ֵ���
�ʵ���װ�۸�![]() ʱ���������Ԥ��ֵ���.
ʱ���������Ԥ��ֵ���.

 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�