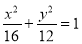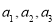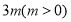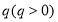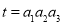Question

某公司计划在今年内同时出售变频空调机和智能洗衣机，由于这两种产品的市场需求量非常大，有多少就能销售多少，因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量，以使得总利润达到最大。已知对这两种产品有直接限制的因素是资金和劳动力，经调查，得到关于这两种产品的有关数据如下表：

资 金	每台单位产品所需资金（百元）	月资金供应量 （百元）
空调机	洗衣机
成 本	30	20	300
劳动力（工资）	5	10	110
每台产品利润	6	8

试问：怎样确定两种货物的月供应量，才能使总利润最大？最大利润是多少?

 

Answer 1

当月供应量为空调机4台，洗衣机9台时，可获最大利润9600元。

【解析】

试题分析：这是一个典型的线性规划问题，首先确定变量，设空调机、洗衣机的月供应量分别是，台，总利润是，根据题意列出线性约束条件，写出目标函数表达式，画出可行域，找出最优解。

试题解析：设空调机、洗衣机的月供应量分别是，台，总利润是，可得

线性约束条件为：，即 4分

目标函数为 5分

作出二元一次不等式组所表示的平面区域，即可行域

8分

考虑，将它变形为，这是斜率为、随变化的一族平行直线，是直线在轴上的截距，当取最大值时，的值最大，当然直线要与可行域相交，由图可得，当直线经过可行域上的点时，截距最大，即最大． 11分

解方程组，得的坐标为 12分

∴(百元) 13分

答：当月供应量为空调机4台，洗衣机9台时，可获最大利润9600元。 14分

考点：线性规划.